
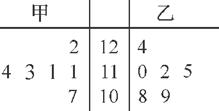
某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔一小时抽一包产品,称其重量(单位:g)是否合格,分别记录抽查数据,获得重量数据茎叶图,如图所示.
(1) 根据样本数据,计算甲、乙两个车间产品重量的均值与方差,并说明哪个车间的产品的重量相对稳定;
(2) 若从乙车间6件样品中随机抽取两件,求所抽取两件样品重量之差不超过2 g的概率.
(1) 设甲、乙两个车间产品重量的均值分别为 ,
,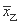 ,方差分别为
,方差分别为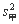 ,
,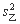 ,
,
则 =
=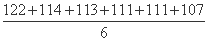 =113,
=113,
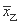 =
=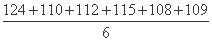 =113.
=113.
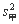 =
=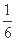 ×[(122-113)2+(114-113)2+(113-113)2+(111-113)2+(111-113)2+(107-113)2]=21,
×[(122-113)2+(114-113)2+(113-113)2+(111-113)2+(111-113)2+(107-113)2]=21,
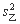 =
=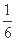 ×[(124-113)2+(110-113)2+(112-113)2+(115-113)2+(108-113)2+(109-113)2]≈29.33,
×[(124-113)2+(110-113)2+(112-113)2+(115-113)2+(108-113)2+(109-113)2]≈29.33,
因为 =
=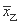 ,
,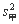 <
<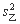 ,所以甲车间的产品的重量相对稳定.
,所以甲车间的产品的重量相对稳定.
(2) 从乙车间6件样品中随机抽取两件,结果共有15种:(124,110),(124,112),(124,115),(124,108),(124,109),(110,112),(110,115),(110,108),(110,109),(112,115),(112,108),(112,109),(115,108),(115,109),(108,109).
设所抽取两件样品重量之差不超过2g的事件为A,则事件A共有4个结果:(110,112),(110,108),(110,109),(108,109).
所以P(A)=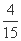 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
f(x)是定义在(0,+∞)上的非负可导函数,且满足xf′(x)+f(x)≤0,对任意正数a,b,若a<b,则必有( )
A.af(b)≤bf(a) B bf(a)≤af(b) C. af(a)<bf(b) D.bf(b)<af(a)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知口袋中有3个白球、4个红球,每次从口袋中任取一球,如果取到红球,那么继续取球;如果取到白球,就停止取球,记取球的次数为X.
(1) 若取到红球再放回,求X不大于2的概率;
(2) 若取出的红球不放回,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
在公差为d的等差数列{an}中,已知a1=10,且a1,2a2+2,5a3成等比数列.
(1) 求d,an;
(2) 若d<0,求|a1|+|a2|+|a3|+…+|an|.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在三棱柱ABC A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
(1) 求证:AA1⊥平面ABC;
(2) 求二面角A1 BC1
BC1 B1的平面角的余弦值;
B1的平面角的余弦值;
(3) 求证:在线段BC1存在点D,使得AD⊥A1B;并求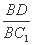 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com