练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图,在三棱柱ABCA1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.

    (1) 求证:AA1⊥平面ABC;

    (2) 求二面角A1BC1B1的平面角的余弦值;

    (3) 求证:在线段BC1存在点D,使得AD⊥A1B;并求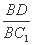的值.


     (1) 证明略　(2) 　(3)


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


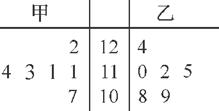
    某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔一小时抽一包产品,称其重量(单位:g)是否合格,分别记录抽查数据,获得重量数据茎叶图,如图所示.

    (1) 根据样本数据,计算甲、乙两个车间产品重量的均值与方差,并说明哪个车间的产品的重量相对稳定;

    (2) 若从乙车间6件样品中随机抽取两件,求所抽取两件样品重量之差不超过2 g的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     如图,已知圆A,圆B都经过点C,BC是圆A的切线,圆B交AB于点D,连接CD并延长、交圆A于点E,连接AE.求证:DE·DC=2AD·DB.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知正方体ABCDA1B1C1D1中,E,F分别为BB1,CD的中点,求证:D1F⊥平面ADE.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


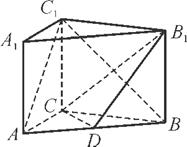
    如图,在直三棱柱ABCA1B1C1中,AC=3,BC=4,AB=5,AA1=4.

    (1) 设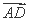=λ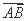,异面直线AC1与CD所成角的余弦值为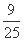,求λ的值;

    (2) 若点D是AB的中点,求二面角DCB1B的平面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设A=,B=,X=,试解方程AX=B.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知矩阵M=对应的变换将点A(1,1)变为A'(0,2),将曲线C:xy=1变为曲线C',求:

    (1) 实数a,b的值;

    (2) 曲线C'的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知实数x,y满足那么z=·的最小值为　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在路边安装路灯,灯柱AB与地面垂直,灯杆BC与灯柱AB所在平面与道路垂直,且∠ABC=120°,路灯C采用锥形灯罩,射出的光线如图中阴影部分所示,已知∠ACD=60°,路宽AD=24 m,设灯柱高AB=h(m),∠ACB=θ(30°≤θ≤45°).

    (1) 求灯柱的高h(用θ表示);

    (2) 若灯杆BC与灯柱AB所用材料相同,记此用料长度和为S,求S关于θ的函数解析式,并求出S的最小值.

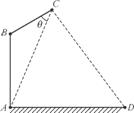
    　(第11题)

    查看答案和解析>>

    同步练习册答案