练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

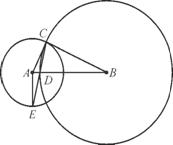
     如图,已知圆A,圆B都经过点C,BC是圆A的切线,圆B交AB于点D,连接CD并延长、交圆A于点E,连接AE.求证:DE·DC=2AD·DB.


    　(第7题)

    由已知,AC⊥BC,因为∠ACD+∠BCD=90°,

    AC=AE,

    BC=BD,

    所以∠ACD=∠E,∠BCD=∠BDC.

    又∠ADE=∠BDC,所以∠E+∠ADE=90°,

    所以AE⊥AB.

    延长DB交☉B于点F,连接FC,则DF=2DB,∠DCF=90°,

    所以∠ACD=∠F,所以∠E=∠F,

    所以RtADE∽RtCDF,

    所以=,所以DE·DC=AD·DF.

    又DF=2DB,所以DE·DC=2AD·DB.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知不等式(x+y)·≥9对任意正实数x,y恒成立,那么正实数a的最小值为　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在公差为d的等差数列{an}中,已知a1=10,且a1,2a2+2,5a3成等比数列.

    (1) 求d,an;

    (2) 若d<0,求|a1|+|a2|+|a3|+…+|an|.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     (2-)8的展开式中不含x4项的系数的和为　　　　.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图,∠PAQ是直角,圆O与AP相切于点T,与AQ相交于B,C两点.求证:BT平分∠OBA.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若两个球的表面积之比为1∶4,则这两个球的体积之比为　　　　.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是　　　　寸. 

    (注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸;③台体的体积公式是V台体=h(S+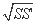+S'),其中S',S分别为上、下底面面积,h为台体高)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图,在三棱柱ABCA1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.

    (1) 求证:AA1⊥平面ABC;

    (2) 求二面角A1BC1B1的平面角的余弦值;

    (3) 求证:在线段BC1存在点D,使得AD⊥A1B;并求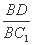的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     在△ABC中,角A,B,C所对的边长分别为a,b,c,设向量x=(sinB,sinC),y=(cosB,cosC),z=(cosB,-cosC),若z∥(x+y),则tanB+tanC=　　　　. 

    查看答案和解析>>

    同步练习册答案