
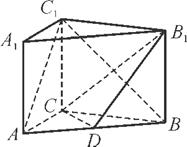
如图,在直三棱柱ABC A1B1C1中,AC=3,BC=4,AB=5,AA1=4.
A1B1C1中,AC=3,BC=4,AB=5,AA1=4.
(1) 设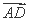 =λ
=λ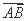 ,异面直线AC1与CD所成角的余弦值为
,异面直线AC1与CD所成角的余弦值为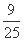 ,求λ的值;
,求λ的值;
(2) 若点D是AB的中点,求二面角D CB1
CB1 B的平面角的余弦值.
B的平面角的余弦值.
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
已知口袋中有3个白球、4个红球,每次从口袋中任取一球,如果取到红球,那么继续取球;如果取到白球,就停止取球,记取球的次数为X.
(1) 若取到红球再放回,求X不大于2的概率;
(2) 若取出的红球不放回,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是 寸.
(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸;③台体的体积公式是V台体= h(S+
h(S+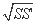 +S'),其中S',S分别为上、下底面面积,h为台体高)
+S'),其中S',S分别为上、下底面面积,h为台体高)
查看答案和解析>>
科目:高中数学 来源: 题型:
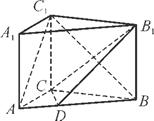
如图,在直三棱柱ABC A1B1C1中,AC=3,BC=4,AB=5,AA1=4,
A1B1C1中,AC=3,BC=4,AB=5,AA1=4,
(1) 求证: AC⊥BC1;
(2) 在AB上是否存在点D,使得AC1⊥CD
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在三棱柱ABC A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
(1) 求证:AA1⊥平面ABC;
(2) 求二面角A1 BC1
BC1 B1的平面角的余弦值;
B1的平面角的余弦值;
(3) 求证:在线段BC1存在点D,使得AD⊥A1B;并求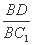 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com