Question

2．已知函数f（x）=|$\frac{1}{4}$x²+$\frac{1}{2}$ax+$\frac{1}{4}$|（a＞1）
（Ⅰ）（i）求函数f（x）的单调递增区间；
     （ii）若函数g（x）=f（x）-$\frac{1}{2}$x-a恰有三个零点，求a的值；
（Ⅱ）记M（a，t）为函数f（x）在区间[t，t+2]（t∈R）上的最大值，求M（a，t）的最小值．

Answer 1

分析 （Ⅰ）画出函数的图象，令f（x）=0，求出方程的解，从而求出函数的单调区间；（ii）应有y=$\frac{1}{2}$x+a与y=-（$\frac{1}{4}$x²+$\frac{1}{2}$ax+$\frac{1}{4}$）相切，求出a的值即可；
（Ⅱ）通过换元，令x+a=u，则h（u）=$\frac{1}{4}$|u²-（a²-1）|，其中u∈[t+a，t+a+2]，令s=（t+a）∈R，则M为h（u）在区间[s，s+2]上的最大值，通过讨论①当0∈[s，s+2]时，②当0∉[s，s+2]时的情况，求出M（a，t）的最小值即可．

解答 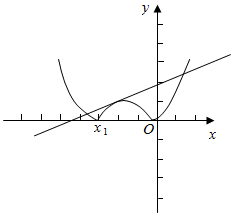解：（Ⅰ）函数f（x）的图象如图示：
（i）由f（x）=0得x₁=-a-$\sqrt{{a}^{2}-1}$，x₂=-a+$\sqrt{{a}^{2}-1}$，
从而单调递减区间是（-a-$\sqrt{{a}^{2}-1}$，-a），（-a+$\sqrt{{a}^{2}-1}$，+∞）；
（ii）若满足题意需满足函数f（x）的图象与直线y=$\frac{1}{2}$x+a恰有三个交点，
考虑到直线y=$\frac{1}{2}$x+a不经过（x₁，0），
∴应有y=$\frac{1}{2}$x+a与y=-（$\frac{1}{4}$x²+$\frac{1}{2}$ax+$\frac{1}{4}$）相切，
此时，$\frac{1}{4}$x²+$\frac{1}{2}$ax+$\frac{1}{4}$=-$\frac{1}{2}$x-a有2个相等的根，解得：a=2，
另一方面，a=2时，g（x）恰有3个零点：-3，-1-2$\sqrt{2}$，-1+2$\sqrt{2}$，
综上，a=2；
（Ⅱ）f（x）=$\frac{1}{4}$|（x+a）²-（a²-1）|，x∈[t，t+2]，（t∈R），
令x+a=u，则h（u）=$\frac{1}{4}$|u²-（a²-1）|，其中u∈[t+a，t+a+2]，
令s=（t+a）∈R，则M为h（u）在区间[s，s+2]上的最大值，
①当0∈[s，s+2]时，结合函数h（u）的图象得：M=max{h（s），h（0），h（s+2）}，
∴$\left\{\begin{array}{l}{M≥h（s）≥\frac{1}{4}{[s}^{2}-{（a}^{2}-1）]}\\{M≥h（s+2）≥\frac{1}{4}{[（s+2）}^{2}-{（a}^{2}-1）]}\\{2M≥2h（0）=\frac{1}{4}（{2a}^{2}-2）}\end{array}\right.$，
将三式相加得4M≥$\frac{1}{4}$[（s+2）²+s²]=$\frac{1}{2}$[（s+1）²+1]≥$\frac{1}{2}$，从而M≥$\frac{1}{8}$，
②当0∉[s，s+2]时，类似的2M≥$\frac{1}{4}$|（s+2）²-s²|=|s+1|＞1，此时，M＞$\frac{1}{2}$，
另一方面，当s=-1，a=$\frac{\sqrt{6}}{2}$，即a=$\frac{\sqrt{6}}{2}$，t=-1-$\frac{\sqrt{6}}{2}$时：
函数f（x）在区间[-1-$\frac{\sqrt{6}}{2}$，1-$\frac{\sqrt{6}}{2}$]上的最大值M=$\frac{1}{8}$，
综上，当t和a变化时，M（a，t）的最小值是$\frac{1}{8}$．

点评 本题考查了函数的单调性问题，考查函数的零点问题以及绝对值的应用，是一道综合题．