过两直线x+3y-10=0和y=3x的交点,并且与原点距离为1的直线方程为 .
【答案】
分析:联解两直线方程,得交点为P(1,3).再分直线l与x轴是否垂直加以讨论,结合到直线的距离公式列式,可解出满足条件的直线方程.
解答:解:联解方程组
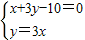
,得x=1,y=3
∴直线x+3y-10=0和y=3x的交点为P(1,3)
当直线l与x轴垂直时,方程为x=1,到原点距离为1
当直线l与x轴不垂直时,设方程为y-3=k(x-1)
即kx-y+3-k=0
由d=
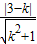
=1,解之得k=

,
可得此时直线方程为

x-y+3-

=0,即4x-3y+5=0
综上所述,满足条件的直线l的方程为x=1或4x-3y+5=0
故答案为:x=1或4x-3y+5=0
点评:本题给出经过两条直线交点的直线,在它到原点距离等于1的情况下求直线方程.着重考查了点到直线的距离公式和直线的方程等知识,属于基础题.

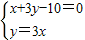 ,得x=1,y=3
,得x=1,y=3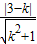 =1,解之得k=
=1,解之得k= ,
, x-y+3-
x-y+3- =0,即4x-3y+5=0
=0,即4x-3y+5=0

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案