
分析 在△ABC中,由余弦定理可得AC,求出∠ACD=15°,在△ACD中,∠D=120°,由正弦定理可得AD.
解答 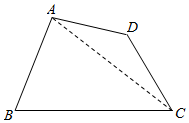 解:连接AC,在△ABC中,由余弦定理可得AC=$\sqrt{1+4-2×1×2×cos60°}$=$\sqrt{3}$,
解:连接AC,在△ABC中,由余弦定理可得AC=$\sqrt{1+4-2×1×2×cos60°}$=$\sqrt{3}$,
∴BC2=AB2+AC2,
∴∠BAC=90°,
∴∠ACB=30°,
∴∠ACD=15°.
在△ACD中,∠D=120°,由正弦定理可得AD=$\frac{\sqrt{3}sin15°}{sin120°}$=$\frac{\sqrt{6}-\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{6}-\sqrt{2}}{2}$.
点评 本题考查余弦定理、正弦定理的运用,考查学生的计算能力,求出AC,∠ACD是关键.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,2] | B. | (0,+∞) | C. | (0,2] | D. | [0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [${4}^{\frac{1}{3}}$,+∞) | B. | [${4}^{\frac{1}{3}}$,6] | C. | [4,+∞) | D. | [3,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (-1,0) | C. | (-2,-1) | D. | (-6,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
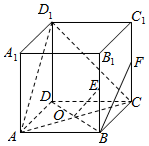 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别是棱BB1、CC1的中点,AC与BD交于点O.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别是棱BB1、CC1的中点,AC与BD交于点O.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
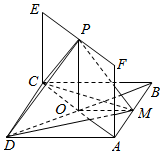 如图所示,已知正方形ABCD所在平面垂直于矩形ACEF所在的平面,BD与AC的交点为O,M,P分别为AB,EF的中点,AB=2,AF=1.
如图所示,已知正方形ABCD所在平面垂直于矩形ACEF所在的平面,BD与AC的交点为O,M,P分别为AB,EF的中点,AB=2,AF=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 (重点中学做)ABCD-A1B1C1D1是棱长为1的正方体,一个质点从A出发沿正方体的面对角线运动,每走完一条面对角线称为“走完一段”,质点的运动规则如下:运动第i段与第i+2所在直线必须是异面直线(其中i是正整数).质点走完的第99段与第1段所在的直线所成的角是( )
(重点中学做)ABCD-A1B1C1D1是棱长为1的正方体,一个质点从A出发沿正方体的面对角线运动,每走完一条面对角线称为“走完一段”,质点的运动规则如下:运动第i段与第i+2所在直线必须是异面直线(其中i是正整数).质点走完的第99段与第1段所在的直线所成的角是( )| A. | 0° | B. | 30° | C. | 60° | D. | 90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com