练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．（重点中学做）ABCD-A1B1C1D1是棱长为1的正方体，一个质点从A出发沿正方体的面对角线运动，每走完一条面对角线称为“走完一段”，质点的运动规则如下：运动第i段与第i+2所在直线必须是异面直线（其中i是正整数）．质点走完的第99段与第1段所在的直线所成的角是（　　）
    A．0°B．30°C．60°D．90°

    分析 由质点的运动规则得到质点走过6段后又回到起点A，可以看作以4为周期，由此能求出质点走完的第99段与第1段所在的直线所成的角．

    解答 解：不妨设质点运行路线为AB1→B1C→CD1→D1A
    即走过4段后又回到起点A，可以看作以4为周期，
    ∵99=4×24+3，
    ∴质点走完的第99段与第1段所在的直线分别为AB1与CD1，
    ∵AB1⊥CD1，
    ∴质点走完的第99段与第1段所在的直线所成的角是90°．
    故选：D．

    点评 本题考查异面直线所成角的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    9．在平面四边形ABCD中，若AB=1，BC=2，B=60°，C=45°，D=120°，则AD=$\frac{\sqrt{6}-\sqrt{2}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知变量x，y满足$\left\{\begin{array}{l}{x-y-2≤0}\\{x+2y-5≥0}\\{y-2≤0}\end{array}\right.$，则2x+y的最大值为（　　）
    A．4B．7C．10D．12

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．设全集U={-2，-1，0，1，2}，集合M={-1，0，1}，N={x|x2-x-2=0}，则（∁UM）∩N=（　　）
    A．{2}B．{-1}C．{-2，-1，2}D．{-1，1}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．如图，E，F分别是正方形ABCD的边BC，CD的中点，沿图中虚线折起来，它能形成怎样的几何体？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

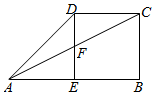    4．如图，ABCD是直角梯形，AB∥CD，AB=2CD=2，CD=BC，E是AB的中点，DE⊥AB，F是AC与DE的交点．
    （Ⅰ）求sin∠CAD的值；
    （Ⅱ）求△ADF的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

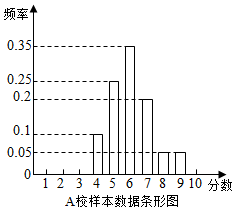    11．某市组织高一全体学生参加计算机操作比赛，等级分为1至10分，随机调阅了A、B两所学校各60名学生的成绩，得到样本数据如表：
    B校样本数据统计表：
    成绩（分）12345678910
    人数（个）000912219630
    （Ⅰ）计算两校样本数据的均值和方差，并根据所得数据进行比较．
    （Ⅱ）从A校样本数据成绩分别为7分、8分和9分的学生中按分层抽样方法抽取6人，若从抽取的6人中任选2人参加更高一级的比赛，求这2人成绩之和大于或等于15的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．函数f（x）=lg（4-x2）的定义域为（-2，2）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．在平面直角坐标系xOy中，已知点P（1，$\frac{3}{2}$）在椭圆C：$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上，P到椭圆C的两个焦点的距离之和为4．
    （1）求椭圆C的方程；
    （2）若点M，N是椭圆C上的两点，且四边形POMN是平行四边形，求点M，N的坐标．

    查看答案和解析>>

    同步练习册答案