
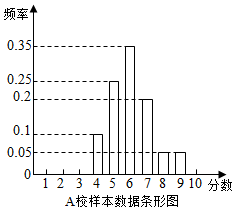
 某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:
某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:| 成绩(分) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数(个) | 0 | 0 | 0 | 9 | 12 | 21 | 9 | 6 | 3 | 0 |
分析 (Ⅰ)分别求出A校样本的平均成绩、方差和B校样本的平均成绩、方差,从而得到两校学生的计算机成绩平均分相同,A校学生的计算机成绩比较稳定,总体得分情况比较集中,
(Ⅱ)根据分成抽样求出故抽取的7分有4人即为A,B,C,D,8分和9分的学生中各为1人,记为a,b,一一列举所有的基本事件,再找到满足条件的基本事件,根据概率公式计算即可.
解答 解:(Ⅰ)从A校样本数据的条形图知:
成绩分别为4分、5分、6分、7分、8分、9分的学生分别有:
6人、15人、21人、12人、3人、3人
A校样本的平均成绩为:$\overline{{x}_{A}}$=$\frac{1}{60}$(4×6+5×15+6×21+7×12+8×3+9×3)=6(分),
A校样本的方差为SA2=$\frac{1}{60}$[6(4-6)2+15(5-6)2+21(6-6)2+12(7-6)2+3(8-6)2+3(9-6)2]=1.5.
从B校样本数据统计表知:
B校样本的平均成绩为:$\overline{{x}_{B}}$=$\frac{1}{60}$(4×9+5×12+6×21+7×9+8×6+9×3=6(分),
B校样本的方差为SB2=$\frac{1}{60}$[9(4-6)2+12(5-6)2+21(6-6)2+9(7-6)2+6(8-6)2+3(9-6)2]=1.8.
∵$\overline{{x}_{A}}$=$\overline{{x}_{B}}$,SA2<SB2,
∴两校学生的计算机成绩平均分相同,A校学生的计算机成绩比较稳定,总体得分情况比较集中.
(Ⅱ)A校样本数据成绩分别为7分、8分和9分的学生中按分层抽样方法抽取6人,由于7分、8分、9分的学生分别有12人,3人,3人,
故抽取的7分有6×$\frac{12}{12+3+3}$=4人即为A,B,C,D,8分和9分的学生中各为1人,记为a,b,
故从抽取的6人中任选2人参加更高一级的比赛,共有AB,AC,AD,BC,BD,CD,Aa,Ba,Ca,Da,Ab,Bb,Cb,Db,ab共有15种,
其中2人成绩之和大于或等于15的分的有Aa,Ba,Ca,Da,Ab,Bb,Cb,Db,ab共9种,
故这2人成绩之和大于或等于15的概率P=$\frac{9}{15}$=$\frac{3}{5}$
点评 本题考查平均数、方差的求法及应用,考查概率的求法,解题时要认真审题,注意频率分布直方图的应用,是中档题.


科目:高中数学 来源: 题型:解答题
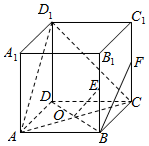 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别是棱BB1、CC1的中点,AC与BD交于点O.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别是棱BB1、CC1的中点,AC与BD交于点O.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{1}{2}$] | B. | [$\frac{1}{2}$,1] | C. | [$\frac{1}{3}$,$\frac{1}{2}$] | D. | $(\frac{1}{3},\frac{1}{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 (重点中学做)ABCD-A1B1C1D1是棱长为1的正方体,一个质点从A出发沿正方体的面对角线运动,每走完一条面对角线称为“走完一段”,质点的运动规则如下:运动第i段与第i+2所在直线必须是异面直线(其中i是正整数).质点走完的第99段与第1段所在的直线所成的角是( )
(重点中学做)ABCD-A1B1C1D1是棱长为1的正方体,一个质点从A出发沿正方体的面对角线运动,每走完一条面对角线称为“走完一段”,质点的运动规则如下:运动第i段与第i+2所在直线必须是异面直线(其中i是正整数).质点走完的第99段与第1段所在的直线所成的角是( )| A. | 0° | B. | 30° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com