
分析 由z1(2+i)=5i(i为虚数单位),可得z1=2i+1,设z2=a+bi,(a,b∈R),再利用复数的运算法则、复数为实数、纯虚数的充要条件即可得出.
解答 解:∵z1(2+i)=5i(i为虚数单位),
∴z1(2+i)(2-i)=5i(2-i),∴z1=i(2-i)=2i+1,
设z2=a+bi,(a,b∈R),
∵复数z2满足z1+z2=1+2i+(a+bi)=(1+a)+(2+b)i为实数,
∴2+b=0,解得b=-2.
∵z1•z2=(1+2i)(a-2i)=a+4+(2a-1)i为纯虚数,
∴a+4=0,2a-1≠0,解得a=-4.
∴复数z2=-4-2i.
点评 本题考查了复数的运算法则、复数为实数及纯虚数的充要条件,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {-1} | C. | {-2,-1,2} | D. | {-1,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
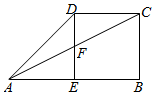 如图,ABCD是直角梯形,AB∥CD,AB=2CD=2,CD=BC,E是AB的中点,DE⊥AB,F是AC与DE的交点.
如图,ABCD是直角梯形,AB∥CD,AB=2CD=2,CD=BC,E是AB的中点,DE⊥AB,F是AC与DE的交点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
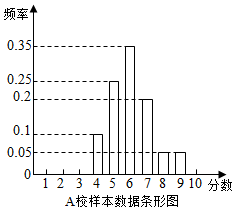 某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:
某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:| 成绩(分) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数(个) | 0 | 0 | 0 | 9 | 12 | 21 | 9 | 6 | 3 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
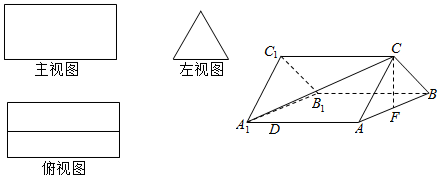
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com