
分析 由题意可得6=p+q,分类讨论以确定$\frac{1}{p}$+$\frac{9}{q}$的最小值为m=3-$\frac{1}{4}$,从而可得b1=$\frac{1}{2}$,b2=$\frac{2}{3}$,利用数学归纳法可证明bn=$\frac{n}{n+1}$,从而化简$\frac{{b}_{n}}{{n}^{2}}$=$\frac{n}{(n+1){n}^{2}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,从而利用裂项求和法求得.
解答 解:∵在公差不为0的等差数列{an}中,a2+a4=ap+aq,
∴2+4=p+q,
当p=1,q=5时,$\frac{1}{p}$+$\frac{9}{q}$=3-$\frac{1}{5}$,
当p=2,q=4时,$\frac{1}{p}$+$\frac{9}{q}$=3-$\frac{1}{4}$,
当p=3,q=3时,$\frac{1}{p}$+$\frac{9}{q}$=3+$\frac{1}{3}$,
当p=4,q=2时,$\frac{1}{p}$+$\frac{9}{q}$=$\frac{1}{4}$+$\frac{9}{2}$,
当p=5,q=1时,$\frac{1}{p}$+$\frac{9}{q}$=$\frac{1}{5}$+9,
故$\frac{1}{p}$+$\frac{9}{q}$的最小值为m=3-$\frac{1}{4}$,
故b1=$\frac{2}{11}$m=$\frac{2}{11}$•$\frac{11}{4}$=$\frac{1}{2}$,
∵2bn+1-bn•bn+1=1,
∴bn+1=$\frac{1}{2-{b}_{n}}$,
∴b2=$\frac{1}{2-\frac{1}{2}}$=$\frac{2}{3}$,
由数学归纳法可证明bn=$\frac{n}{n+1}$,
$\frac{{b}_{n}}{{n}^{2}}$=$\frac{n}{(n+1){n}^{2}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
故b1+$\frac{{b}_{2}}{{2}^{2}}$+$\frac{{b}_{3}}{{3}^{2}}$+…+$\frac{{b}_{100}}{{100}^{2}}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$.
点评 本题考查了等差数列的性质的应用及分类讨论的思想应用,同时考查了裂项求和法的应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
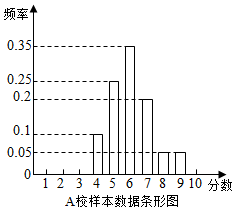 某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:
某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:| 成绩(分) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数(个) | 0 | 0 | 0 | 9 | 12 | 21 | 9 | 6 | 3 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$a | B. | $\frac{\sqrt{3}}{2}$a | C. | $\frac{\sqrt{6}}{3}$a | D. | $\frac{\sqrt{6}}{6}$a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ①②④ | C. | ①④ | D. | ①③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com