
| A. | [0,$\frac{1}{2}$] | B. | [$\frac{1}{2}$,1] | C. | [$\frac{1}{3}$,$\frac{1}{2}$] | D. | $(\frac{1}{3},\frac{1}{2}]$ |
分析 命题q:(x-a)(x-a-1)≤0,解得a≤x≤a+1.由于¬p是¬q的必要不充分条件,可得q是p的必要不充分条件.即可得出.
解答 解:命题q:(x-a)(x-a-1)≤0,解得a≤x≤a+1.
∵¬p是¬q的必要不充分条件,
∴q是p的必要不充分条件.
∴$\left\{\begin{array}{l}{a≤\frac{1}{2}}\\{1≤a+1}\end{array}\right.$,且等号不能同时成立.
解得$0≤a≤\frac{1}{2}$.
则实数a的取值范围是$[0,\frac{1}{2}]$.
故选:A.
点评 本题考查了不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 7 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {-1} | C. | {-2,-1,2} | D. | {-1,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
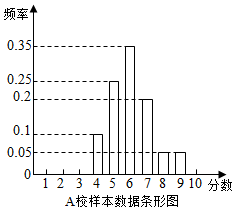 某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:
某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:| 成绩(分) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数(个) | 0 | 0 | 0 | 9 | 12 | 21 | 9 | 6 | 3 | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com