
分析 Sn=(-1)n-1•n,可得:a1=S1=1.当n≥2时,an=Sn-Sn-1,可得an=(-1)n-1(2n-1),对n分类讨论,利用(an+1-p)(an-p)<0恒成立,即可解出.
解答 解:∵Sn=(-1)n-1•n,
∴a1=S1=1.
当n≥2时,an=Sn-Sn-1=(-1)n-1•n-(-1)n-2(n-1)=(-1)n-1(2n-1),当n=1时也成立,
∴an=(-1)n-1(2n-1),
当n为偶数时,(an+1-p)(an-p)<0化为:[(2n+1)-p][-(2n-1)-p]<0,-(2n-1)<p<2n+1,可得-3<p<5.
当n为奇数时,(an+1-p)(an-p)<0化为:[-(2n+1)-p][(2n-1)-p]<0,-(2n+1)<p<2n-1,可得-3<p<1.
∴$\left\{\begin{array}{l}{-3<p<5}\\{-3<p<1}\end{array}\right.$,
解得-3<p<1.
故答案为:(-3,1).
点评 本题考查了递推公式、不等式的解法、分类讨论方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{4}^{n}-1}{3}$ | B. | $\frac{({2}^{n}-1)^{2}}{3}$ | C. | 4n-1 | D. | (2n-1)2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,2] | B. | (0,+∞) | C. | (0,2] | D. | [0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [${4}^{\frac{1}{3}}$,+∞) | B. | [${4}^{\frac{1}{3}}$,6] | C. | [4,+∞) | D. | [3,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
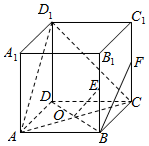 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别是棱BB1、CC1的中点,AC与BD交于点O.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别是棱BB1、CC1的中点,AC与BD交于点O.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{1}{2}$] | B. | [$\frac{1}{2}$,1] | C. | [$\frac{1}{3}$,$\frac{1}{2}$] | D. | $(\frac{1}{3},\frac{1}{2}]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com