
| A. | -$\frac{5}{2}$ | B. | -$\frac{2}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{5}{2}$ |
分析 由复数z的实部为0且虚部不为0求得tanθ,再把sinθcosθ转化为含有tanθ的代数式得答案.
解答 解:∵复数z=(sinθ-2cosθ)+(sinθ+2cosθ)i是纯虚数,
∴$\left\{\begin{array}{l}{sinθ-2cosθ=0}\\{sinθ+2cosθ≠0}\end{array}\right.$,解得tanθ=2.
则sinθcosθ=$\frac{sinθcosθ}{si{n}^{2}θ+co{s}^{2}θ}=\frac{tanθ}{ta{n}^{2}θ+1}=\frac{2}{{2}^{2}+1}=\frac{2}{5}$.
故选:C.
点评 本题考查复数的基本概念,考查了三角函数的化简求值,是基础题.


 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 111 110 | B. | 1 111 111 | C. | 1 111 112 | D. | 1 111 113 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{1-{m}^{2}}}{|m|}$ | B. | $\frac{\sqrt{1-{m}^{2}}}{-m}$ | C. | $\frac{\sqrt{1+{m}^{2}}}{m}$ | D. | $\frac{\sqrt{1-{m}^{2}}}{m}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
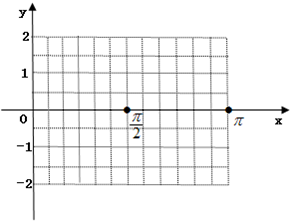 已知函数f(x)=2cos2x+2$\sqrt{3}$sinxcosx-1.
已知函数f(x)=2cos2x+2$\sqrt{3}$sinxcosx-1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com