Question

【题目】如图1，在正方形ABCD中，点E，F分别是AB，BC的中点，BD与EF交于点H，G为BD中点，点R在线段BH上，且 =λ（λ＞0）．现将△AED，△CFD，△DEF分别沿DE，DF，EF折起，使点A，C重合于点B（该点记为P），如图2所示．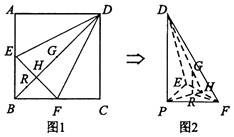

（I）若λ=2，求证：GR⊥平面PEF；
（Ⅱ）是否存在正实数λ，使得直线FR与平面DEF所成角的正弦值为 ？若存在，求出λ的值；若不存在，请说明理由．

Answer 1

【答案】（I）证明：由题意，PE，PF，PD三条直线两两垂直，∴PD⊥平面PEF， 图1中，EF∥AC，∴GB=2GH，
∵G为BD中点，∴DG=2GH．
图2中，∵ =2，∴△PDH中，GR∥PD，
∴GR⊥平面PEF；
（Ⅱ）解：由题意，建立如图所示的坐标系，设PD=4，则P（0，0，0），F（2，0，0），E（0，2，0），D（0，0，4），∴H（1，1，0），
∵ =λ，∴R（ ， ，0），
∴ =（ ，﹣ ，0），
∵ =（2，﹣2，0）， =（0，2，﹣4），
设平面DEF的一个法向量为 =（x，y，z），则 ，取 =（2，2，1），
∵直线FR与平面DEF所成角的正弦值为 ，
∴ = ，
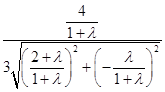∴λ= ，
∴存在正实数λ= ，使得直线FR与平面DEF所成角的正弦值为 ．

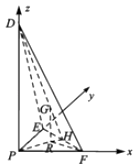
【解析】（I）若λ=2，证明PD⊥平面PEF，GR∥PD，即可证明：GR⊥平面PEF；（Ⅱ）建立如图所示的坐标系，求出平面DEF的一个法向量，利用直线FR与平面DEF所成角的正弦值为 ，建立方程，即可得出结论．
【考点精析】本题主要考查了空间角的异面直线所成的角的相关知识点，需要掌握已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则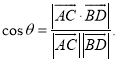才能正确解答此题．