
分析 (Ⅰ)求导数f′(x)=xex,这样根据导数符号即可得出f(x)的单调区间,并可求出f(x)的最小值;
(Ⅱ)可构造函数$h(x)=f(x)-g(x)=(x-1){e}^{x}+1-\frac{1}{3}a{x}^{3}$$-\frac{1}{2}{x}^{2}$,求导数得到h′(x)=x(ex-ax-1),这样只需判断φ(x)=ex-ax-1的符号,求导数φ′(x)=ex-a,可知ex≥1,这样讨论a:a≤1,和a>1,每种情况下判断φ(x),h′(x)的符号,从而看是否得出h(x)≥0,这样即可得出实数a的取值范围.
解答 解:(Ⅰ)f′(x)=xex;
∴x<0时,f′(x)<0,x>0时,f′(x)>0;
∴f(x)的单调递减区间为(-∞,0),单调递增区间为(0,+∞),且f(x)的最小值为f(0)=0;
(Ⅱ)构造函数h(x)=f(x)-g(x)=$(x-1){e}^{x}+1-\frac{1}{3}a{x}^{3}-\frac{1}{2}{x}^{2}$,x∈[0,+∞);
∴h′(x)=xex-ax2-x=x(ex-ax-1);
∵x∈[0,+∞),
∴ex-ax-1的符号就是h′(x)的符号;
设φ(x)=ex-ax-1,x∈[0,+∞),φ′(x)=ex-a;
∵x∈[0,+∞),∴ex≥1;
①a≤1时,φ′(x)=ex-a≥0,φ(x)在[0,+∞)上是增函数,又φ(0)=0,
∴φ(x)≥0;
∴h′(x)≥0,h(x)在[0,+∞)上是增函数,又h(0)=0,
∴h(x)≥0;
∴a≤1符合题意;
②a>1时,令φ′(x)=0得,x=lna>0,在[0,lna)上φ′(x)<0,φ(x)是减函数φ(0)=0;
∴x∈(0,lna)时,φ(x)<0,∴h′(x)<0,h(x)在(0,lna)上是减函数;
∴h(x)<0;
∴a>1不合题意;
综上所述,实数a的取值范围为(-∞,1].
点评 考查基本初等函数求导公式,积的导数的计算公式,根据导数符号求函数单调区间的方法,以及根据导数符号求函数最值的方法和过程,以及函数单调性定义,构造函数的方法.


科目:高中数学 来源: 题型:解答题
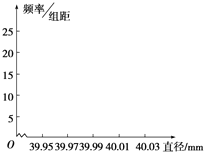 某制造商为运动会生产一批直径为40mm的乒乓球,现随机抽样检查20只,测得每只球的直径(单位:mm,保留两位小数)如下:
某制造商为运动会生产一批直径为40mm的乒乓球,现随机抽样检查20只,测得每只球的直径(单位:mm,保留两位小数)如下:| 分组 | 频数 | 频率 | $\frac{频率}{组距}$ |
| [39.95,39.97) | 2 | 0.10 | 5 |
| [39.97,39.99) | 4 | 0.20 | 10 |
| [39.99,40.01) | 10 | 0.50 | 25 |
| [40.01,40.03] | 4 | 0.20 | 10 |
| 合计 | 20 | 1 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
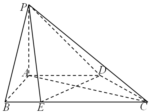 如图,在四棱锥P-ABCD中,直线PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=2AB=2AD=4BE=4.
如图,在四棱锥P-ABCD中,直线PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=2AB=2AD=4BE=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3f(2)<2f(3) | B. | 2f(3)<3f(2) | C. | 3f(4)<4f(3) | D. | 2f(3)<3f(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com