
ЗжЮі НЋвбжЊВЛЕШЪНСНБпЦНЗНЕУЕНСНИіЯђСПЕФЪ§СПЛ§ЕФВЛЕШЪНЃЌРћгУЯђСПЕФЭЖгАЕФЖЈвхЕУЕНЗЖЮЇЃЎ
НтД№ НтЃКгЩвбжЊЃК|$\overrightarrow a|=13$ЃЌ|$\overrightarrow b|=1$ЃЌ|$\overrightarrow a-5\overrightarrow b|Ём12$ЃЌЕУЕН$|\overrightarrow{a}-5\overrightarrow{b}{|}^{2}Ём144$ЃЌЫљвд169-10$\overrightarrow{a}•\overrightarrow{b}$+25Ём144ЃЌЫљвд$\overrightarrow{a}•\overrightarrow{b}$Ён5Ыљвд$\overrightarrow b$дк$\overrightarrow a$ЩЯЕФЭЖгА$\overrightarrow{b}•cosЃМ\overrightarrow{a}ЃЌ\overrightarrow{b}ЃО$$Ён\frac{5}{13}$ЃЛгжcosЃМ$\overrightarrow{a}ЃЌ\overrightarrow{b}$ЃОЁм1ЃЌЫљвд$\overrightarrow b$дк$\overrightarrow a$ЩЯЕФЭЖгАЕФШЁжЕЗЖЮЇЪЧ[$\frac{5}{13}$ЃЌ1]ЃЛ
ЙЪД№АИЮЊЃК$[\frac{5}{13}ЃЌ1]$ЃЎ
ЕуЦР БОЬтПМВщСЫЯђСПЕФФЃЕФМЦЫувдМАЯђСПЕФЭЖгАЃЛЙиМќЪЧНЋвбжЊВЛЕШЪНЦНЗНЕУЕНЪ§СПЛ§ЕФЗЖЮЇЃЌНјвЛВНЕУЕНЭЖгАЕФЗЖЮЇЃЌЪєгкЛљДЁЬтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
 ФГбЇаЃЮЊЕїВщИпжаШ§ФъМЖФаЩњЕФЩэИпЧщПіЃЌбЁШЁСЫ500УћФаЩњзїЮЊбљБОЃЌШчЭМЪЧДЫДЮЕїВщЭГМЦЕФСїГЬЭМЃЌШєЪфГіЕФНсЙћЪЧ380ЃЌдђЩэИпдк170cmвдЯТЕФЦЕТЪЮЊ0.24ЃЎ
ФГбЇаЃЮЊЕїВщИпжаШ§ФъМЖФаЩњЕФЩэИпЧщПіЃЌбЁШЁСЫ500УћФаЩњзїЮЊбљБОЃЌШчЭМЪЧДЫДЮЕїВщЭГМЦЕФСїГЬЭМЃЌШєЪфГіЕФНсЙћЪЧ380ЃЌдђЩэИпдк170cmвдЯТЕФЦЕТЪЮЊ0.24ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
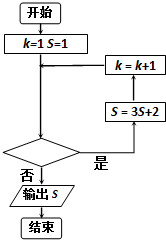
| AЃЎ | kЃМ5ЃП | BЃЎ | kЃО7ЃП | CЃЎ | kЁм5ЃП | DЃЎ | kЁм6ЃП |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | $\sqrt{3}$ | BЃЎ | $\sqrt{3}$+1 | CЃЎ | $\frac{\sqrt{3}-1}{2}$ | DЃЎ | $\frac{\sqrt{3}+1}{2}$ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com