
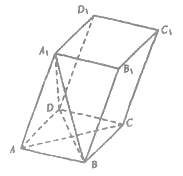
【题目】在四棱柱![]() 中,底面ABCD是菱形,且
中,底面ABCD是菱形,且![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的大小.
的大小.
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题分析:(1)要证明面面垂直,先证明线面垂直,即线垂直于平面内的两条相交直线,因为底面菱形,所以对角线![]() ,易得
,易得![]() ,所以
,所以![]() ,这样就证明了直线
,这样就证明了直线![]() 垂直于平面内的两条相交直线,这样线面垂直;(2)根据(1)的证明,可以O为原点建立空间直角坐标系,分别得到两个平面的法向量,根据公式
垂直于平面内的两条相交直线,这样线面垂直;(2)根据(1)的证明,可以O为原点建立空间直角坐标系,分别得到两个平面的法向量,根据公式![]() ,得到二面角的大小.
,得到二面角的大小.
试题解析:(1)因为![]() ,所以
,所以![]() 和
和![]() 均为正三角形,于是
均为正三角形,于是![]() .设AC与BD的交点为O,则
.设AC与BD的交点为O,则![]() ,又ABCD是菱形,所以AC⊥BD,
,又ABCD是菱形,所以AC⊥BD,
而![]() ,所以BD⊥平面
,所以BD⊥平面![]() ,故平面
,故平面![]() 平面
平面![]() .
.
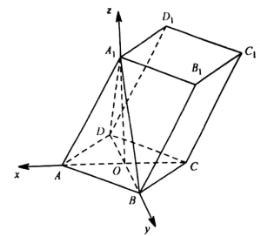
(2)由![]() ,及
,及![]() 知
知![]() ,又由
,又由![]() ,
,
得![]() ,故
,故![]() ,
,
于是![]() ,从而
,从而![]() ,结合
,结合![]() 得
得
![]() 底面ABCD.如图,建立空间直角坐标系,则
底面ABCD.如图,建立空间直角坐标系,则![]() ,
,
![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,由
,由 得
得![]()
令x=1,得![]() ,平面
,平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设平面![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则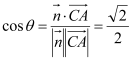 ,故
,故![]() .
.


科目:高中数学 来源: 题型:
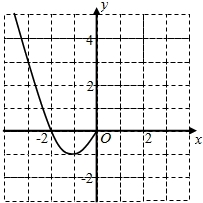
【题目】已知函数是定义在上的偶函数,且当时,.
(1)现已画出函数在轴左侧的图象,如图所示,请补出完整函数的图象,并根据图象写出函数的增区间;
(2)写出函数的解析式和值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知推理:“因为所有的金属都能够导电,而铜能导电,所以铜是金属”.则下列结论正确的是( )
A. 此推理大前提错误 B. 此推理小前提错误
C. 此推理的推理形式错误 D. 此推理无错误
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某校九年级1600名学生的体能情况,随机抽查了部分学生,测试1分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图,根据统计图的数据,下列结论错误的是( )
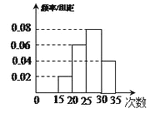
A.该校九年级学生1分钟仰卧起坐的次数的中位数为26.25次
B.该校九年级学生1分钟仰卧起坐的次数的众数为27.5次
C.该校九年级学生1分钟仰卧起坐的次数超过30次的人数约有320人
D.该校九年级学生1分钟仰卧起坐的次数少于20次的人数约有32人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100 名电视观众,相关的数据如下表(单位:人)所示:
收看文艺节目 | 收看新闻节目 | 总计 | |
20至40岁 | 40 | 18 | 58 |
大于40岁 | 15 | 27 | 42 |
总计 | 55 | 45 | 100 |
由表中数据直观分析,收看新闻节目的观众是否与年龄有关:__________.(填“是”或“否”)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】算法具有明确性,其明确性指的是
A. 算法一定包含输入、输出
B. 算法的步骤是有限的
C. 算法的每个步骤是具体的、可操作的
D. 以上说法均不正确
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系
B.在线性回归分析中,相关系数r的值越大,变量间的相关性越强
C.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
D.在回归分析中,![]() 为0.98的模型比
为0.98的模型比![]() 为0.80的模型拟合的效果好
为0.80的模型拟合的效果好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各式中正确的有 .(把你认为正确的序号全部写上)
(1)![]() ;
;
(2)已知![]() 则
则![]() ;
;
(3)函数![]() 的图象与函数
的图象与函数![]() 的图象关于原点对称;
的图象关于原点对称;
(4)函数![]() 是偶函数;
是偶函数;
(5)函数![]() 的递增区间为
的递增区间为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com