【题目】已知f（x）是定义在R上的偶函数，且x≤0时，f（x）= 
（1﹣x）．
（1）求f（0），f（1）；
（2）求函数f（x）的解析式．
【答案】
（1）解：f（x）是定义在R上的偶函数，且x≤0时，f（x）= 
（1﹣x）．
f（0）=0，
f（1）=f（﹣1）= （1+1）=﹣1
（2）解：f（x）是定义在R上的偶函数，且x≤0时，f（x）= （1﹣x）．
x＞0时，f（x）=f（﹣x）=l 1+x）．
可得：f（x）=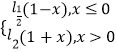 
【解析】（1）利用函数的奇偶性的性质，求解函数值即可．（2）利用函数的奇偶性以及已知条件真假求解函数的解析式即可．
【考点精析】认真审题，首先需要了解函数奇偶性的性质(在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇)．
科目：高中数学 来源： 题型：
【题目】（本小题满分10分）选修4—4：坐标系与参数方程
在直角坐标系xOy中，圆C的参数方程
为参数）．以O为极点，x轴的非负半轴为极轴建立极坐标系．
（1）求圆C的极坐标方程；
（2）直线
的极坐标方程是
，射线
与圆C的交点为O、P，与直线
的交点为Q，求线段PQ的长．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】运货卡车以每小时
千米的速度匀速行驶
千米（
）.假设汽油的价格是每升
元，而汽车每小时耗油
升，司机的工资是每小时
元.
（1）求这次行车总费用
关于
的表达式；
（2）当
为何值时，这次行车的总费用最低？并求出最低费用的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】经国务院批复同意，重庆成功入围国家中心城市，某校学生社团针对“重庆的发展环境”对20名学生进行问卷调查打分（满分100分），得到如图所示茎叶图：
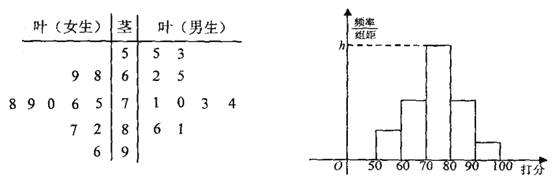
（Ⅰ）计算女生打分的平均分，并用茎叶图的数字特征评价男生、女生打分谁更分散；
（Ⅱ）如图按照打分区间
、
、
、
、
绘制的直方图中，求最高矩形的高
；
（Ⅲ）从打分在70分以下（不含70分）的同学中抽取3人，求有女生被抽中的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设集合
.如果对于
的每一个含有
个元素的子集
， 
中必有4个元素的和等于
，称正整数
为集合
的一个“相关数”.
（Ⅰ）当
时，判断5和6是否为集合
的“相关数”，说明理由；
（Ⅱ）若
为集合
的“相关数”，证明： 
；
（Ⅲ）给定正整数
.求集合
的“相关数” 
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
