【题目】已知F1 ， F2分别是长轴长为2 的椭圆C： + =1（a＞b＞0）的左右焦点，A1 ， A2是椭圆C的左右顶点，P为椭圆上异于A1 ， A2的一个动点，O为坐标原点，点M为线段PA2的中点，且直线PA2与OM的斜率之积恒为﹣ ．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设过点F1且不与坐标轴垂直的直线l交椭圆于A，B两点，线段AB的垂直平分线与x轴交于点N，点N横坐标的取值范围是（﹣ ，0），求线段AB长的取值范围．

参考答案：

【答案】解：（Ⅰ）由题意可知2a=2 ，则a= ，设P（x0 ， y0），
∵直线PA与OM的斜率之积恒为﹣ ，∴ × =﹣ ，
∴ + =1，
∴b=1，
椭圆C的方程 ；
（Ⅱ）设直线l：y=k（x+1），A（x1 ， y1），B（x2 ， y2），
联立直线与椭圆方程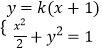： ，得：（2k2+1）x2+4k2x+2k2﹣2=0，
则x1+x2=﹣ ，x1x2= ，
则y1+y2=k（x1+x2+2）= ，
∴AB中点Q（﹣ ， ），
QN直线方程为：y﹣ =﹣ （x+ ）=﹣ x﹣ ，
∴N（﹣ ，0），由已知得﹣ ＜﹣ ＜0，
∴0＜2k2＜1，
∴|AB|= =
= = （1+ ），
∵ ＜＜12k2+1＜1，
∴|AB|∈（ ，2 ），
线段AB长的取值范围（ ，2 ）
【解析】（Ⅰ）利用椭圆Q的长轴长为2 ，求出a= ，设P（x0 ， y0），通过直线PA与OM的斜率之积恒为，﹣ ．化简求出b，即可得到椭圆方程；（Ⅱ）将直线方程代入椭圆方程，由此利用韦达定理、中点坐标公式、直线方程、弦长公式，能求出线段AB长的取值范围．

关闭