练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    命题p：∀x∈(1，＋∞)，函数f(x)＝|log2x|的值域为[0，＋∞)；命题q：∃m≥0，使得y＝sin mx的周期小于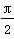，试判断p∨q，p∧q，綈p的真假性．


    解：对于命题p，当f(x)＝|log2x|＝0时，log2x＝0，即x＝1,1∉(1，＋∞)，故命题p为假命题．对于命题q，y＝sin mx的周期T＝<，即|m|>4，故m<－4或m>4，故存在，m≥0，使得命题q成立，所以p且q为假命题．故p∨q为真命题，p∧q为假命题，綈p为真命题．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    若函数y＝sin(ωx＋φ)(ω>0)的部分图像如图，则ω＝(　　)

    A．5                                                             B．4

    C．3                                                             D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设集合Sn＝{1,2,3，…，n}，若X⊆Sn，把X的所有元素的乘积称为X的容量(若X中只有一个元素，则该元素的数值即为它的容量，规定空集的容量为0)．若X的容量为奇(偶)数，则称X为Sn的奇(偶)子集．则S4的所有奇子集的容量之和为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    将a2＋b2＋2ab＝(a＋b)2改写成全称命题是(　　)

    A．∃a，b∈R，a2＋b2＋2ab＝(a＋b)2

    B．∃a<0，b>0，a2＋b2＋2ab＝(a＋b)2

    C．∀a>0，b>0，a2＋b2＋2ab＝(a＋b)2

    D．∀a，b∈R，a2＋b2＋2ab＝(a＋b)2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知命题p：“∀x∈[1,2]都有x2≥a”．命题q：“∃x0∈R，使得x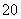＋2ax0＋2－a＝0成立”，若命题“p∧q”是真命题，则实数a的取值范围为(　　)

    A．(－∞，－2]                    B．(－2,1)

    C．(－∞，－2]∪{1}               D．[1，＋∞)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列函数中，不满足f(2x)＝2f(x)的是(　　)

    A．f(x)＝|x|                                         B．f(x)＝x－|x|

    C．f(x)＝x＋1                                     D．f(x)＝－x

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    具有性质：f＝－f(x)的函数，我们称为满足“倒负”变换的函数，下列函数：

    ①y＝x－；②y＝x＋；③y＝其中满足“倒负”变换的函数是(　　)

    A．①②　　                                       B．①③　　　C．②③　　　D．①

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，一个几何体的正视图和侧视图是腰长为1的等腰三角形，俯视图是一个圆及其圆心，当这个几何体的体积最大时圆的半径是 （    ）

        A．       B．    C．    D．

     

     

     

     

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝2x，x∈R.

    当m取何值时方程|f(x)－2|＝m有一个解？两个解？

    查看答案和解析>>

    同步练习册答案