练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)＝2x，x∈R.

    当m取何值时方程|f(x)－2|＝m有一个解？两个解？


    解：令F(x)＝|f(x)－2|＝|2x－2|，

    G(x)＝m，画出F(x)的图像如图所示．

    由图像看出，当m＝0或m≥2时，函数F(x)与G(x)的图像只有一个交点，原方程有一个解；

    当0<m<2时，

    函数F(x)与G(x)的图像有两个交点，

    原方程有两个解．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    命题p：∀x∈(1，＋∞)，函数f(x)＝|log2x|的值域为[0，＋∞)；命题q：∃m≥0，使得y＝sin mx的周期小于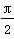，试判断p∨q，p∧q，綈p的真假性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设，若仅有一个常数c使得对于任意的，都有满足方程，这时，的取值的集合为                  。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设f(x)是(－∞，＋∞)上的奇函数，f(x＋2)＝－f(x)，

    当0≤x≤1时，f(x)＝x.

    (1)求f(3)的值；

    (2)当－4≤x≤4时，求f(x)的图像与x轴所围成图形的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数y＝的图像大致是(　　)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知二次函数的图像如图所示，那么此函数的解析式可能是(　　)

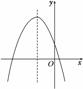    A．y＝－x2＋2x＋1

    B．y＝－x2－2x－1

    C．y＝－x2－2x＋1

    D．y＝x2＋2x＋1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知幂函数f(x)＝x(m2＋m)－1(m∈N*)，经过点(2，)，试确定m的值，并求满足条件f(2－a)>f(a－1)的实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数y＝f(x)是函数y＝ax(a＞0，且a≠1)的反函数，且f(2)＝1，则f(x)＝(　　)

    A．log2x                                             B.

    C．logx                                           D．2x－2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f1(x)＝sin x＋cos x，记f2(x)＝f1′(x)，f3(x)＝f2′(x)，…，fn(x)＝fn－1′(x)(n∈N*，n≥2)，则＝________.

    查看答案和解析>>

    同步练习册答案