
���� ���������������F1Ϊ��-1��0������$P��t��\sqrt{t}��$�����${k_{P{F_1}}}=\frac{{\sqrt{t}}}{t+1}$������ԲM���ҽ���ΪF2��1��0�������a��c��Ȼ�������ԲM�������ʣ�
������A��x1��y1����B��x2��y2����ֱ��l�ķ���Ϊx=my-1������Բ����������Τ�ﶨ��������OB����|OA|=|OC|֪S��ABC=2S��AOB������������ʽ��ͨ������$\frac{1}{b}��1$����$1��a��\sqrt{2}$������$0��\frac{1}{b}��1$��$a��\sqrt{2}$����⺯������ֵ����ʽ���ɣ�
��� �⣺���������⣬��F1Ϊ��-1��0������$P��t��\sqrt{t}��$����${k_{P{F_1}}}=\frac{{\sqrt{t}}}{t+1}$��
��${k_{P{F_1}}}=��\sqrt{x}��'{|_{x=t}}=��\frac{1}{{2\sqrt{x}}}��{|_{x=t}}=\frac{1}{{2\sqrt{t}}}$������$\frac{{\sqrt{t}}}{t+1}=\frac{1}{{2\sqrt{t}}}$�����t=1����P��1��1����
����ԲM���ҽ���ΪF2��1��0������$2a=|P{F_1}|+|P{F_2}|=\sqrt{5}+1$����$a=\frac{{\sqrt{5}+1}}{2}$��
�ְ뽹��c=1��������ԲM��������Ϊ$e=\frac{c}{a}=\frac{{\sqrt{5}-1}}{2}$������5�֣�
������Ϊ��ԲM�İ뽹��c=1������a2-b2=1����A��x1��y1����B��x2��y2����
ֱ��l�ķ���Ϊx=my-1��
�ɷ�����$\left\{\begin{array}{l}\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\\ x=my-1\end{array}\right.$��ȥx�ã���a2+b2m2��y2-2b2my+b2��1-a2��=0��
��${y_1}+{y_2}=\frac{{2{b^2}m}}{{{a^2}+{b^2}{m^2}}}{y_1}{y_2}=\frac{{{b^2}��1-{a^2}��}}{{{a^2}+{b^2}{m^2}}}=-\frac{b^4}{{{a^2}+{b^2}{m^2}}}$������7�֣�
����OB����|OA|=|OC|֪S��ABC=2S��AOB��
��${S_{��ABC}}=|O{F_1}|•|{y_1}-{y_2}|=\sqrt{{{��{y_1}+{y_2}��}^2}-4{y_1}{y_2}}=\frac{{2a{b^2}\sqrt{{m^2}+1}}}{{{a^2}+{b^2}{m^2}}}$����9�֣�
��$\sqrt{{m^2}+1}=t$����m2=t2-1��t��1������${S_{��ABC}}=\frac{{2a{b^2}t}}{{{a^2}+{b^2}��{t^2}-1��}}=\frac{{2a{b^2}t}}{{1+{b^2}{t^2}}}=\frac{{2a{b^2}}}{{{b^2}t+\frac{1}{t}}}$��
����$\frac{1}{b}��1$����$1��a��\sqrt{2}$����${b^2}t+\frac{1}{t}��2b=2\sqrt{{a^2}-1}$��
���ҽ���$t=\frac{1}{b}$����$m=��\sqrt{\frac{{2-{a^2}}}{{{a^2}-1}}}$ʱ��$S��a��={��{S_{��ABC}}��_{max}}=a\sqrt{{a^2}-1}$������10�֣�
����$0��\frac{1}{b}��1$����$a��\sqrt{2}$����$f��t��={b^2}t+\frac{1}{t}$����t��1ʱ��$f'��t��={b^2}-\frac{1}{t^2}=\frac{{{b^2}{t^2}-1}}{t^2}��0$��
����f��t����[1��+�ޣ��ϵ�������������${[f��t��]_{min}}=f��1��={b^2}+1={a^2}$�����ҽ���t=1��
��m=0ʱ��$S��a��={��{S_{��ABC}}��_{max}}=\frac{{2��{a^2}-1��}}{a}$������12�֣�
���Ͽ�֪��$S��a��=\left\{{\begin{array}{l}{a\sqrt{{a^2}-1}��1��a��\sqrt{2}}\\{\frac{{2��{a^2}-1��}}{a}��a��\sqrt{2}}\end{array}}\right.$����13�֣�
���� ���⿼��ֱ�߳��λ�ù�ϵ��Ӧ�ã����������������������������麯������ֵ��������Ӧ�ã��������������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 32 | B�� | 36 | C�� | 18 | D�� | 86 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 400 | B�� | 410 | C�� | 420 | D�� | 430 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪��Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����һ������ΪF��1��0�����ҹ��㣨-1��$\frac{3}{2}$�����Ҷ���ΪA��������F�Ķ�ֱ��l����Բ����B��C���㣮
��֪��Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����һ������ΪF��1��0�����ҹ��㣨-1��$\frac{3}{2}$�����Ҷ���ΪA��������F�Ķ�ֱ��l����Բ����B��C���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 5 | C�� | 6 | D�� | 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
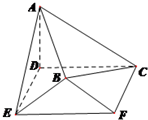 ��ͼ���ڿռ伸����ABCDEF�У�����CDEFΪ���Σ�DE=1��CD=2��AD�͵���CDEF��AD=1��ƽ��BEF�͵���CDEF����BE=BF=$\sqrt{2}$��
��ͼ���ڿռ伸����ABCDEF�У�����CDEFΪ���Σ�DE=1��CD=2��AD�͵���CDEF��AD=1��ƽ��BEF�͵���CDEF����BE=BF=$\sqrt{2}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com