
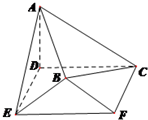
 如图,在空间几何体ABCDEF中,底面CDEF为矩形,DE=1,CD=2,AD⊥底面CDEF,AD=1,平面BEF⊥底面CDEF,且BE=BF=$\sqrt{2}$.
如图,在空间几何体ABCDEF中,底面CDEF为矩形,DE=1,CD=2,AD⊥底面CDEF,AD=1,平面BEF⊥底面CDEF,且BE=BF=$\sqrt{2}$.分析 (Ⅰ) 过点B作BM⊥EF,利用平面与平面垂直的性质,可得BM⊥底面CDEF,利用AD⊥底面CDEF,可得BM∥AD,从而可证明四边形ADMB为平行四边形,即可证明AB∥平面CDEF;
(Ⅱ) 利用等体积转化,即可求几何体A-DBC的体积V.
解答 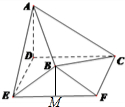 (Ⅰ)证明:过点B作BM⊥EF,
(Ⅰ)证明:过点B作BM⊥EF,
∵平面BEF⊥底面CDEF,且BE=BF=$\sqrt{2}$,
∴M为等腰直角三角形底边EF的中点,
∴BM⊥底面CDEF,
∵AD⊥底面CDEF,
∴BM∥AD,
又∵AD=BM=1,
∴四边形ADMB为平行四边形,∴AB∥DM,
∵AB?底面CDEF,DM?底面CDEF,
∴AB∥平面CDEF…(6分)
(Ⅱ)解:∵${V_{A-BCD}}={V_{B-ADC}}=\frac{1}{3}{S_{△ADC}}•d$(d为三棱锥B-ADC高)
∵DE⊥DC,DE⊥AD,∴DE⊥平面ADC
又∵平面BEF⊥底面CDEF,DE⊥EF,
∴DE⊥平面BEF
∴平面BEF∥平面ADC,
∵d=ED=1,${S_{△ADC}}=\frac{1}{2}×1×2=1$,∴VA-BCD=$\frac{1}{3}×1×1$=$\frac{1}{3}$…(12分)
点评 本题考查平面与平面垂直的性质,考查线面平行的判定,考查三棱锥体积的计算,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 年龄(周岁) | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 身高 | 94.8 | 104.2 | 108.7 | 117.8 | 124.3 | 130.8 | 139.1 |
| A. | 142.8cm | B. | 145.9cm | C. | 149.8cm | D. | 151.7cm |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | f(x)=x+sinx | B. | f(x)=x•sinx | C. | f(x)=x•cosx | D. | f(x)=x(x-$\frac{π}{2}$)(x-$\frac{3π}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (10,+∞)∪{0} | B. | (10,+∞) | C. | (0,10) | D. | (0,10] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com