
分析 (1)把bn+1=1+$\frac{{b}_{n}}{{a}_{n}}$右边通分后两边平方,与an+12=$\frac{({a}_{n}+{b}_{n})^{2}}{{{a}_{n}}^{2}+{{b}_{n}}^{2}}$两边作积即可证得数列{cn}是等差数列,由等差数列的通项公式求其通项公式;
(2)求出数列{cn}的前n项和为Sn,代入$\sum_{i=1}^{n}$ai$\sqrt{{S}_{i}}$整理,利用错位相减法求其和,由不等式$\sum_{i=1}^{n}$ai$\sqrt{{S}_{i}}$≤k-$\frac{\sqrt{2}n}{{2}^{n}}$分离k后求得函数的最大值得答案.
解答 (1)证明:递推关系可变形为:$\frac{1}{{{a}_{n+1}}^{2}}=\frac{{{a}_{n}}^{2}+{{b}_{n}}^{2}}{({a}_{n}+{b}_{n})^{2}}$,${{b}_{n+1}}^{2}=\frac{({a}_{n}+{b}_{n})^{2}}{{{a}_{n}}^{2}}$(n∈N*),
两式相乘得:$\frac{{{b}_{n+1}}^{2}}{{{a}_{n+1}}^{2}}=\frac{{{a}_{n}}^{2}+{{b}_{n}}^{2}}{{{a}_{n}}^{2}}=\frac{{{b}_{n}}^{2}}{{{a}_{n}}^{2}}+1$(n∈N*),即cn+1=cn+1(n∈N*),
又${a}_{1}=2{{b}_{1}}^{2}$,∴${c}_{1}=\frac{{{b}_{1}}^{2}}{{{a}_{1}}^{2}}$.
∴数列{cn}是首项为$\frac{1}{2}$,公差为1的等差数列,
故{cn}的通项公式:${c}_{n}={c}_{1}+(n-1)d=\frac{1}{2}+(n-1)×1=n-\frac{1}{2}$;
(2)解:由(1)知道,${S}_{n}=\frac{(\frac{1}{2}+n-\frac{1}{2})n}{2}=\frac{{n}^{2}}{2}$,${a}_{n}={a}_{1}×(\frac{1}{2})^{n-1}=\frac{1}{{2}^{n-1}}$,
∴$\sum_{i=1}^{n}$ai$\sqrt{{S}_{i}}$=$\sum_{i=1}^{n}\frac{1}{{2}^{i-1}}•\frac{i}{\sqrt{2}}=\sqrt{2}\sum_{i=1}^{n}\frac{i}{{2}^{i}}$.
记${T}_{n}=\sum_{i=1}^{n}\frac{i}{{2}^{i}}=\frac{1}{2}+\frac{2}{{2}^{2}}+\frac{3}{{2}^{3}}+…+\frac{n}{{2}^{n}}$ ①
$\frac{1}{2}{T}_{n}=\frac{1}{{2}^{2}}+\frac{2}{{2}^{3}}+\frac{3}{{2}^{4}}+…+\frac{n}{{2}^{n+1}}$ ②
由①-②得:$\frac{1}{2}{T}_{n}=\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{n}}-\frac{n}{{2}^{n+1}}$
=$\frac{\frac{1}{2}(1-(\frac{1}{2})^{n})}{1-\frac{1}{2}}-\frac{n}{{2}^{n+1}}=1-\frac{2+n}{{2}^{n+1}}$.
∴${T}_{n}=2-\frac{2+n}{{2}^{n}}$.
∴$\sqrt{2}(2-\frac{2+n}{{2}^{n}})≤k-\frac{\sqrt{2}n}{{2}^{n}}$,
即对于任意的正整数n,不等式$k≥2\sqrt{2}-\frac{2\sqrt{2}}{{2}^{n}}$恒成立,∴k≥$(2\sqrt{2}-\frac{2\sqrt{2}}{{2}^{n}})_{max}$,
当n=1时,$(2\sqrt{2}-\frac{2\sqrt{2}}{{2}^{n}})_{max}=\sqrt{2}$.
∴k的范围是[$\sqrt{2},+∞$).
点评 本题考查数列递推式,考查了等差关系的确定,训练了错位相减法求数列的和,考查了数列的函数特性,属中高档题.


科目:高中数学 来源: 题型:解答题
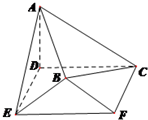 如图,在空间几何体ABCDEF中,底面CDEF为矩形,DE=1,CD=2,AD⊥底面CDEF,AD=1,平面BEF⊥底面CDEF,且BE=BF=$\sqrt{2}$.
如图,在空间几何体ABCDEF中,底面CDEF为矩形,DE=1,CD=2,AD⊥底面CDEF,AD=1,平面BEF⊥底面CDEF,且BE=BF=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知棱长为1的正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,点P,Q分别在棱A1B1、A1D1上,且A1P=A1Q=x(0<x<1),设平面MEF∩平面MPQ=l,则下列结论中错误的是( )
已知棱长为1的正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,点P,Q分别在棱A1B1、A1D1上,且A1P=A1Q=x(0<x<1),设平面MEF∩平面MPQ=l,则下列结论中错误的是( )| A. | l∥平面ABCD | |
| B. | l⊥AC | |
| C. | 存在x0∈(0,1),使平面MEF与平面MPQ垂直 | |
| D. | 当x变化时,l是定直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com