

分析 由已知中的三视图,可知该几何体是一个三棱柱切去一个三棱锥所得的组合体,分别求出各个面的面积相加,可得组合体的表面积;分别求出体积后相减,可得组合体的体积.
解答 解:由已知中的三视图,可知该几何体是一个三棱柱切去一个三棱锥所得的组合体,其直观图如图所示: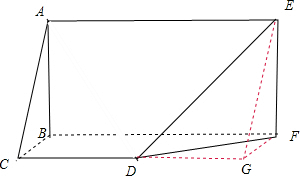
平面ABFE的面积为:32,
平面BCDF的面积为:24,
平面ABC的面积为:8,
平面DEF的面积为:8$\sqrt{2}$,
平面ADE的面积为:16$\sqrt{2}$,
平面ACD的面积为:8$\sqrt{2}$,
故组合体的表面积为:$64+32\sqrt{2}$,\
棱柱ABC-EFG的体积为:64,
棱锥D-EFG的体积为:$\frac{32}{3}$,
故组合体的体积为:$\frac{160}{3}$,
故答案为:$64+32\sqrt{2}$,$\frac{160}{3}$.
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:高中数学 来源: 题型:选择题
| A. | ②③ | B. | ①②③ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “若$x=\frac{π}{3}$,则$sinx=\frac{{\sqrt{3}}}{2}$”的逆命题为真 | |
| B. | a,b,c为实数,若a>b,则ac2>bc2 | |
| C. | 命题p:?x∈R,使得x2+x-1<0,则?p:?x∈R,使得x2+x-1>0 | |
| D. | 若命题?p∧q为真,则p假q真 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
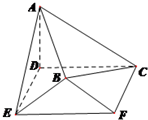 如图,在空间几何体ABCDEF中,底面CDEF为矩形,DE=1,CD=2,AD⊥底面CDEF,AD=1,平面BEF⊥底面CDEF,且BE=BF=$\sqrt{2}$.
如图,在空间几何体ABCDEF中,底面CDEF为矩形,DE=1,CD=2,AD⊥底面CDEF,AD=1,平面BEF⊥底面CDEF,且BE=BF=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com