
【题目】已知椭圆![]() 的上顶点为
的上顶点为![]() ,离心率为
,离心率为![]() . 抛物线
. 抛物线![]() 截
截![]() 轴所得的线段长为
轴所得的线段长为![]() 的长半轴长.
的长半轴长.
(1)求椭圆![]() 的方程;
的方程;
(2)过原点的直线![]() 与
与![]() 相交于
相交于![]() 两点,直线
两点,直线![]() 分别与
分别与![]() 相交于
相交于![]() 两点
两点
证明:以![]() 为直径的圆经过点
为直径的圆经过点![]() ;
;
记![]() 和
和![]() 的面积分别是
的面积分别是![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)①证明见解析,②
;(2)①证明见解析,②![]() .
.
【解析】试题分析:(1)![]() 中,令
中,令![]() 得
得![]() ,
,![]() , 又
, 又![]() ,则
,则![]() ,从而
,从而![]() ,进而可得椭圆
,进而可得椭圆![]() 的方程;(2)设出直线方程,与抛物线方程联立,消去
的方程;(2)设出直线方程,与抛物线方程联立,消去![]() ,根据韦达定理以及平面向量数量积公式可证明
,根据韦达定理以及平面向量数量积公式可证明![]() 恒等于零,从而可得以
恒等于零,从而可得以![]() 为直径的圆经过定点
为直径的圆经过定点![]() ;设直线
;设直线![]() :
:![]() ,显然
,显然![]() ,由
,由![]() ,利用弦长公式可得
,利用弦长公式可得![]() ,同理
,同理![]() ,从而可得
,从而可得![]() ,直线与椭圆方程联立,利用弦长公式求出
,直线与椭圆方程联立,利用弦长公式求出![]() ,从而求得
,从而求得![]() ,从而可得两面积比,利用基本不等式求解即可.
,从而可得两面积比,利用基本不等式求解即可.
试题解析:(1)已知.![]() 中,令
中,令![]() 得
得![]() ,
,![]() ,
,
又![]() ,则
,则![]() ,从而
,从而![]() ,
,
椭圆![]() 的方程为:
的方程为:![]() ,
,
(2)直线![]() 的斜率显然存在,设
的斜率显然存在,设![]() 方程为
方程为![]() .由
.由![]() 得
得![]()
设![]()
![]() ,
,
由已知![]() ,所以
,所以![]() .
.
![]() ,
,
故以![]() 为直径的圆经过点
为直径的圆经过点![]() .
.
设直线![]() :
:![]() ,显然
,显然![]() ,由
,由![]() ,得
,得![]() ,
,![]() 或
或![]() ,
,
![]() ,则
,则![]() ,
,
由知/span>![]() ,直线
,直线![]() :
:![]()
那么![]() ,
,
由![]() 得
得![]() ,解得
,解得![]() 或,
或,![]()
![]() ,则
,则![]() ,
,
由知,直线![]() :
:![]() ,
,
那么![]() ,
,
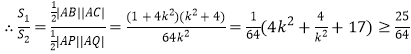 ,
,
当且仅当![]() 时等号成立,即
时等号成立,即![]() 最小值为
最小值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】石嘴山市第三中学高三年级统计学生的最近20次数学周测成绩,现有甲、乙两位同学的20次成绩如茎叶图所示:

(1)根据茎叶图求甲、乙两位同学成绩的中位数,并将同学乙的成绩的频率分布直方图填充完整;
(2)现从甲、乙两位同学的不低于140分的成绩中任意选出2个成绩,记事件![]() 为“其中2个成绩分别属于不同的同学”,求事件
为“其中2个成绩分别属于不同的同学”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的离心率与双曲线
的离心率与双曲线![]() 的离心率互为倒数,且过点
的离心率互为倒数,且过点![]() .
.
(1)求椭圆C的方程;
(2)过![]() 作两条直线
作两条直线![]() 与圆
与圆![]() 相切且分别交椭圆于M、N两点.
相切且分别交椭圆于M、N两点.
① 求证:直线MN的斜率为定值;
② 求△MON面积的最大值(其中O为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某轮船公司的一艘轮船每小时花费的燃料费与轮船航行速度的平方成正比,比例系数为![]() 轮船的最大速度为15海里
轮船的最大速度为15海里![]() 小时
小时![]() 当船速为10海里
当船速为10海里![]() 小时,它的燃料费是每小时96元,其余航行运作费用(不论速度如何)总计是每小时150元
小时,它的燃料费是每小时96元,其余航行运作费用(不论速度如何)总计是每小时150元![]() 假定运行过程中轮船以速度v匀速航行.
假定运行过程中轮船以速度v匀速航行.
![]() 求k的值;
求k的值;
![]() 求该轮船航行100海里的总费用
求该轮船航行100海里的总费用![]() 燃料费
燃料费![]() 航行运作费用
航行运作费用![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将直线2x-y+λ=0沿x轴向左平移1个单位,所得直线与圆x2+y2+2x-4y=0相切,则实数λ的值为( )
A.-3或7B.-2或8
C.0或10D.1或11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系中,已知点A(1,0)和点B(﹣1,0),![]() ,且∠AOC=x,其中O为坐标原点.
,且∠AOC=x,其中O为坐标原点.

(1)若x=![]() ,设点D为线段OA上的动点,求
,设点D为线段OA上的动点,求![]() 的最小值;
的最小值;
(2)若![]() R,求
R,求![]() 的最大值及对应的x值.
的最大值及对应的x值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com