
【题目】已知椭圆C: ![]() 的离心率与双曲线
的离心率与双曲线![]() 的离心率互为倒数,且过点
的离心率互为倒数,且过点![]() .
.
(1)求椭圆C的方程;
(2)过![]() 作两条直线
作两条直线![]() 与圆
与圆![]() 相切且分别交椭圆于M、N两点.
相切且分别交椭圆于M、N两点.
① 求证:直线MN的斜率为定值;
② 求△MON面积的最大值(其中O为坐标原点).
【答案】(1)![]() (2)①
(2)①![]() ②
②![]()
【解析】试题分析:(1)先求双曲线离心率得椭圆离心率,再将点坐标代入椭圆方程,解方程组得![]() ,(2)①先根据点斜式得直线
,(2)①先根据点斜式得直线![]() 方程,再与椭圆方程联立解得
方程,再与椭圆方程联立解得![]() 坐标,根据直线
坐标,根据直线![]() 与圆
与圆![]() 相切,得斜率相反,同理可得
相切,得斜率相反,同理可得![]() 最后根据斜率公式求斜率,②设直线MN方程,根据原点到直线距离得高,与椭圆方程联立方程组结合韦达定理以及弦长公式得底边边长,最后代入三角形面积公式,利用基本不等式求最值.
最后根据斜率公式求斜率,②设直线MN方程,根据原点到直线距离得高,与椭圆方程联立方程组结合韦达定理以及弦长公式得底边边长,最后代入三角形面积公式,利用基本不等式求最值.
试题解析:(1)可得![]() ,设椭圆的半焦距为
,设椭圆的半焦距为![]() ,所以
,所以![]() ,
,
因为C过点![]() ,所以
,所以![]() ,又
,又![]() ,解得
,解得![]() ,
,
所以椭圆方程为![]() .
.
(2)① 显然两直线![]() 的斜率存在,设为
的斜率存在,设为![]() ,
, ![]() ,
,
由于直线![]() 与圆
与圆![]() 相切,则有
相切,则有![]() ,
,
直线![]() 的方程为
的方程为![]() , 联立方程组
, 联立方程组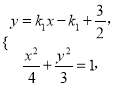
消去![]() ,得
,得![]() ,
,
因为![]() 为直线与椭圆的交点,所以
为直线与椭圆的交点,所以![]() ,
,
同理,当![]() 与椭圆相交时,
与椭圆相交时, ![]() ,
,
所以![]() ,而
,而![]() ,
,
所以直线![]() 的斜率
的斜率![]() .
.
② 设直线![]() 的方程为
的方程为![]() ,联立方程组
,联立方程组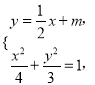 消去
消去![]() 得
得![]() ,
,
所以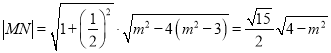 ,
,
原点![]() 到直线的距离
到直线的距离![]() ,
,
![]() 面积为
面积为![]() ,
,
当且仅当![]() 时取得等号.经检验,存在
时取得等号.经检验,存在![]() (
(![]() ),使得过点
),使得过点![]() 的两条直线与圆
的两条直线与圆![]() 相切,且与椭圆有两个交点M,N.
相切,且与椭圆有两个交点M,N.
所以![]() 面积的最大值为
面积的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】己知椭圆W:![]() +
+![]() =1(a>b>0),直线
=1(a>b>0),直线![]() :
:![]() =
=![]() 与
与![]() 轴,
轴,![]() 轴的交点分别是椭圆W的焦点与顶点。
轴的交点分别是椭圆W的焦点与顶点。

(1)求椭圆W的方程;
(2)设直线m:![]() =kx(k≠0)与椭圆W交于P,Q两点,过点P(
=kx(k≠0)与椭圆W交于P,Q两点,过点P(![]() ,
,![]() )作PC⊥轴,垂足为点C,直线
)作PC⊥轴,垂足为点C,直线![]() 交椭圆w于另一点R。
交椭圆w于另一点R。
①求△PCQ面积的最大值;②求出∠QPR的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)已知等差数列{an}的首项a1≠0,前n项和为Sn,且S4+a2=2S3;等比数列{bn}满足b1=a2,b2=a4.
(1)求证:数列{bn}中的每一项都是数列{an}中的项;
(2)若a1=2,设cn=![]() ,求数列{cn}的前n项和Tn;
,求数列{cn}的前n项和Tn;
(3)在(2)的条件下,若有f(n)=log3Tn,求f(1)+f(2)+…+f(n)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科学研究表明:人类对声音有不的感觉,这与声音的强度![]() 单位:瓦
单位:瓦![]() 平方米
平方米![]() 有关
有关![]() 在实际测量时,常用
在实际测量时,常用![]() 单位:分贝
单位:分贝![]() 来表示声音强弱的等级,它与声音的强度I满足关系式:
来表示声音强弱的等级,它与声音的强度I满足关系式:![]() 是常数
是常数![]() ,其中
,其中![]() 瓦
瓦![]() 平方米
平方米![]() 如风吹落叶沙沙声的强度
如风吹落叶沙沙声的强度![]() 瓦
瓦![]() 平方米,它的强弱等级
平方米,它的强弱等级![]() 分贝.
分贝.
![]() 已知生活中几种声音的强度如表:
已知生活中几种声音的强度如表:
声音来源
声音大小 | 风吹落叶沙沙声 | 轻声耳语 | 很嘈杂的马路 |
强度 |
|
|
|
强弱等级 | 10 | m | 90 |
求a和m的值
![]() 为了不影响正常的休息和睡眠,声音的强弱等级一般不能超过50分贝,求此时声音强度I的最大值.
为了不影响正常的休息和睡眠,声音的强弱等级一般不能超过50分贝,求此时声音强度I的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 的图象两相邻对称轴之间的距离是
的图象两相邻对称轴之间的距离是![]() ,若将
,若将![]() 的图象向右平移
的图象向右平移![]() 个单位长度,所得图象对应的函数
个单位长度,所得图象对应的函数![]() 为奇函数.
为奇函数.
(1)求![]() 的解析式;
的解析式;
(2)求![]() 的对称轴及单调增区间;
的对称轴及单调增区间;
(3)若对任意![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an+1=![]() ,设bn=
,设bn=![]() ,n∈N*。
,n∈N*。
(1)证明{bn}是等比数列(指出首项和公比);
(2)求数列{log2bn}的前n项和Tn。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程及曲线
的极坐标方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 交于
交于![]() 两点,过
两点,过![]() 点且垂直于
点且垂直于![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的上顶点为
的上顶点为![]() ,离心率为
,离心率为![]() . 抛物线
. 抛物线![]() 截
截![]() 轴所得的线段长为
轴所得的线段长为![]() 的长半轴长.
的长半轴长.
(1)求椭圆![]() 的方程;
的方程;
(2)过原点的直线![]() 与
与![]() 相交于
相交于![]() 两点,直线
两点,直线![]() 分别与
分别与![]() 相交于
相交于![]() 两点
两点
证明:以![]() 为直径的圆经过点
为直径的圆经过点![]() ;
;
记![]() 和
和![]() 的面积分别是
的面积分别是![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com