
【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 在区间
在区间![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,若对任意的
时,若对任意的![]() 、
、![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 在
在![]() 上的值城为区间
上的值城为区间![]() ,是否存在常数
,是否存在常数![]() ,使得区间
,使得区间![]() 的长度为
的长度为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.(注:区间
的值;若不存在,请说明理由.(注:区间![]() 的长度为
的长度为![]() ).
).
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在常数
;(3)存在常数![]() 或
或![]() 满足题意.
满足题意.
【解析】
(1)求出函数的对称轴,得到函数的单调性,建立关于![]() 的不等式组,解出即可;
的不等式组,解出即可;
(2)依题意,函数![]() 在
在![]() 上的最大值小于等于函数
上的最大值小于等于函数![]() 在
在![]() 上的最小值,此时可以分离变量,也可以直接求解;
上的最小值,此时可以分离变量,也可以直接求解;
(3)通过讨论![]() 的范围,结合函数的单调性以及
的范围,结合函数的单调性以及![]() 、
、![]() 的值,得到关于
的值,得到关于![]() 的方程,解出即可.
的方程,解出即可.
(1)由题意得,函数![]() 的对称轴为
的对称轴为![]() ,
,
故函数![]() 在区间
在区间![]() 上为增函数,
上为增函数,
![]() 函数
函数![]() 在区间
在区间![]() 上存在零点,
上存在零点,
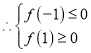 ,即
,即![]() ,解得
,解得![]() ,故实数
,故实数![]() 的取值范围为
的取值范围为![]() ;
;
(2)依题意,函数![]() 在
在![]() 上的最大值小于等于函数
上的最大值小于等于函数![]() 在
在![]() 上的最小值,
上的最小值,
当![]() 时,
时,![]() ,
,
易知,函数![]() 在
在![]() 上的最大值为
上的最大值为![]() .
.
法一:当![]() 时,函数
时,函数![]() 在
在![]() 上为增函数,
上为增函数,
则![]() ,符合题意;
,符合题意;
当![]() 时,函数
时,函数![]() 在
在![]() 上为减函数,
上为减函数,
则![]() ,解得
,解得![]() .
.
综上,实数![]() 的取值范围为
的取值范围为![]() ;
;
法二:依题意,![]() 对任意
对任意![]() 都成立,
都成立,
![]() ,
,![]() ,则
,则![]() ,
,
当![]() 时,则有
时,则有![]() ,显然成立;
,显然成立;
当![]() 时,则
时,则![]() 对任意
对任意![]() 都成立,
都成立,
则函数![]() 为增函数,故
为增函数,故![]() ,即
,即![]() .
.
综上,实数![]() 的取值范围为
的取值范围为![]() ;
;
(3)依题意![]() ,解得
,解得![]() .
.
①当![]() 时,当
时,当![]() 时,
时,![]() ,
,![]() ,即
,即![]() ,
,![]() ,即
,即![]() ,
,
解得![]() ;
;
②当![]() 时,当
时,当![]() 时,
时,![]() ,
,![]() ,
,
![]() ,
,![]() ,解得
,解得![]() ;
;
③当![]() 时,当
时,当![]() 时,
时,![]() ,
,![]() ,
,
![]() ,
,![]() ,解得
,解得![]() ,不符合,舍去;
,不符合,舍去;
综上,存在常数![]() 或
或![]() 满足题意.
满足题意.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,右焦点F是抛物线
,右焦点F是抛物线![]() :
:![]() 的焦点,点
的焦点,点![]() 在抛物线
在抛物线![]() 上
上![]()
![]() 求椭圆
求椭圆![]() 的方程;
的方程;
![]() 已知斜率为k的直线l交椭圆
已知斜率为k的直线l交椭圆![]() 于A,B两点,
于A,B两点,![]() ,直线AM与BM的斜率乘积为
,直线AM与BM的斜率乘积为![]() ,若在椭圆上存在点N,使
,若在椭圆上存在点N,使![]() ,求
,求![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴非负半轴为极轴且取相同的单位长度建立极坐标系.已知点
轴非负半轴为极轴且取相同的单位长度建立极坐标系.已知点![]() 轨迹的参数方程为
轨迹的参数方程为![]() (
(![]() ,
,![]() 为参数),点
为参数),点![]() 在曲线
在曲线![]() 上.
上.
(1)求点![]() 轨迹的普通方程和曲线
轨迹的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若
,若![]() ,则称
,则称![]() 为
为![]() 的“不动点”,若
的“不动点”,若![]() ,则称
,则称![]() 为
为![]() 的“稳定点”,函数
的“稳定点”,函数![]() 的“不动点”和“稳定点”的集合分别记为
的“不动点”和“稳定点”的集合分别记为![]() 和
和![]() ,即
,即![]() ,
,![]() ,那么,
,那么,
(1)求函数![]() 的“稳定点”;
的“稳定点”;
(2)求证:![]() ;
;
(3)若![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设单调函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,如果单调函数
,如果单调函数![]() 使得函数
使得函数![]() 的值域也是
的值域也是![]() ,则称函数
,则称函数![]() 是函数
是函数![]() 的一个“保值域函数”.已知定义域为
的一个“保值域函数”.已知定义域为![]() 的函数
的函数![]() ,函数
,函数![]() 与
与![]() 互为反函数,且
互为反函数,且![]() 是
是![]() 的一个“保值域函数”,
的一个“保值域函数”,![]() 是
是![]() 的一个“保值域函数”,则
的一个“保值域函数”,则![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车行业是碳排放量比较大的行业之一,欧盟从2012年开始就对二氧化碳排放量超过![]()
的![]() 型汽车进行惩罚,某检测单位对甲、乙两类
型汽车进行惩罚,某检测单位对甲、乙两类![]() 型品牌汽车各抽取5辆进行二氧化碳排放量检测,记录如下(单位:
型品牌汽车各抽取5辆进行二氧化碳排放量检测,记录如下(单位:![]() ):
):
甲 | 80 | 110 | 120 | 140 | 150 |
乙 | 100 | 120 |
| 100 | 160 |
经测算发现,乙类![]() 型品牌汽车二氧化碳排放量的平均值为
型品牌汽车二氧化碳排放量的平均值为![]() .
.
(Ⅰ)从被检测的5辆甲类![]() 型品牌车中任取2辆,则至少有1辆二氧化碳排放量超过
型品牌车中任取2辆,则至少有1辆二氧化碳排放量超过![]() 的概率是多少?
的概率是多少?
(Ⅱ)求表中![]() ,并比较甲、乙两类
,并比较甲、乙两类![]() 型品牌汽车二氧化碳排放量的稳定性.
型品牌汽车二氧化碳排放量的稳定性.
![]() ,其中,
,其中,![]() 表示
表示![]() 的平均数,
的平均数,![]() 表示样本数量,
表示样本数量,![]() 表示个体,
表示个体,![]() 表示方差)
表示方差)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且![]() ,
, ![]() .
.
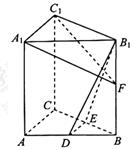
求证:(1)直线DE![]() 平面A1C1F;
平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() 满足对于任意实数
满足对于任意实数![]() ,
,![]() 都有
都有![]() ,且当
,且当![]() 时,
时,![]() ,
,![]() .
.
(1)判断![]() 的奇偶性并证明;
的奇偶性并证明;
(2)判断![]() 的单调性,并求当
的单调性,并求当![]() 时,
时,![]() 的最大值及最小值;
的最大值及最小值;
(3)解关于![]() 的不等式
的不等式![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲、乙两家公司都需要招聘求职者,这两家公司的聘用信息如下:
甲公司 | 乙公司 | ||||||||
职位 | A | B | C | D | 职位 | A | B | C | D |
月薪/千元 | 5 | 6 | 7 | 8 | 月薪/千元 | 4 | 6 | 8 | 10 |
获得相应职位概率 | 0.4 | 0.3 | 0.2 | 0.1 | 获得相应职位概率 | 0.4 | 0.3 | 0.2 | 0.1 |
(1)若两人分别去应聘甲、乙两家公司的C职位,记这两人被甲、乙两家公司的C职位录用的人数和为![]() ,求
,求![]() 的分布列;
的分布列;
(2)根据甲、乙两家公司的聘用信息,如果你是该求职者,你会选择哪一家公司?说明理由。
(3)若小王和小李分别被甲、乙两家公司录用,求小王月薪高于小李的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com