考点:二面角的平面角及求法,组合几何体的面积、体积问题,直线与平面垂直的性质
专题:计算题,作图题,证明题,空间位置关系与距离
分析:(Ⅰ)取AB的中点N,连结MN,CN;从而可证CN⊥AB,MN⊥平面ABC,NM⊥AB,从而得证AB⊥平面MNC,从而得证;
(文科)(Ⅱ)三棱锥A1-ABP的体积可转化为三棱锥P-A1AB的体积,从而求值;
(理科)(Ⅱ)取AC的中点D,连结BD,作DE⊥AP于点E,连结BE;可证∠BED为二面角B-AP-C的平面角,在Rt△BED中求二面角B-AP-C的余弦值.
解答:
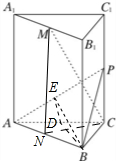
解:(Ⅰ)证明:取AB的中点N,连结MN,CN;
∵底面是正三角形,
∴CN⊥AB,
又∵M为A
1B
1的中点,
∴MN∥AA
1,
又∵AA
1⊥平面ABC,
∴MN⊥平面ABC,
∴NM⊥AB,
又∵MN∩CN=N,MN?平面MNC,CN?平面MNC,
∴AB⊥平面MNC,又∵MC?平面MNC,
∴MC⊥AB.
(文科)(Ⅱ)三棱锥A
1-ABP的体积可转化为三棱锥P-A
1AB的体积,
SA1AB=
×4×2
=4
;
h=CN=4×
=2
,
故V=
×4
×2
=8
.
(理科)(Ⅱ)如图,取AC的中点D,连结BD,作DE⊥AP于点E,连结BE;
∵AA
1⊥平面ABC,BD?平面ABC,
∴AA
1⊥BD,又∵BD⊥AC,
∴BD⊥平面ACP,
∴BD⊥AP,又∵DE⊥AP,
∴AP⊥平面BDE,
∴∠BED为二面角B-AP-C的平面角,
在Rt△BED中,
BD=4×
=2
,
DE=
×
=
,
BE=
=
,
故cos∠BED=
=
.
故二面角B-AP-C的余弦值为
.
点评:本题考查了学生的空间想象力及作图与识图的能力,同时考查了体积的转化,及垂直的应用,属于难题.

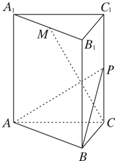 如图,三棱柱ABC-A1B1C1的底面是边长为4正三角形,AA1⊥平面ABC,AA1=2
如图,三棱柱ABC-A1B1C1的底面是边长为4正三角形,AA1⊥平面ABC,AA1=2 解:(Ⅰ)证明:取AB的中点N,连结MN,CN;
解:(Ⅰ)证明:取AB的中点N,连结MN,CN;

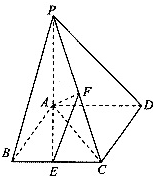 如图,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥面ABCD,AP=AB,E、F分别是BC、PC的中点.
如图,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥面ABCD,AP=AB,E、F分别是BC、PC的中点.