
分析 过G作抛物线的切线,根据导数的几何意义,求得k=±$\sqrt{\frac{2}{p}}$,只需令切线的夹角小于90°即可,则$\sqrt{\frac{2}{p}}$≥1,即可求得p的取值范围.
解答 解:过G点作抛物线的两条切线,设切线方程为y=kx-1,
切点坐标为M(x0,y0),N(-x0,y0),
由y=$\frac{{x}^{2}}{2p}$,y′=$\frac{1}{p}$x,
则由导数的几何意义可知$\left\{\begin{array}{l}{{x}_{0}^{2}={2py}_{0}}\\{{y}_{0}=k{x}_{0}-1}\\{\frac{{x}_{0}}{p}=k}\end{array}\right.$,解得k=±$\sqrt{\frac{2}{p}}$.
$\overrightarrow{MP}•\overrightarrow{MQ}≥0$恒成立,∠AOB≤90°,即∠AGO≤45°,
∴|k|>tan45°=1,即$\sqrt{\frac{2}{p}}$≥1,
解得p≤2,
由p>0,则0<p≤2,
p的取值范围:(0,2],
故答案为:(0,2].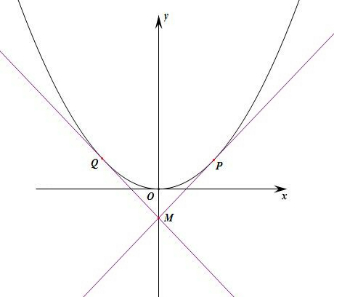
点评 本题考查了直线与抛物线的位置关系,导数的几何意义,考查的数量积,考查数形结合思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组别 | 步数分组 | 频数 |
| A | 5500≤x<6500 | 2 |
| B | 6500≤x<7500 | 10 |
| C | 7500≤x<8500 | m |
| D | 8500≤x<9500 | 2 |
| E | 9500≤x<10500 | n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com