
 的前
的前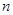 项和是
项和是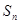 ,满足
,满足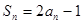 .
. 的通项
的通项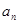 及前
及前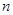 项和
项和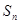 ;
;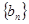 满足
满足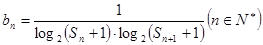 ,求数列
,求数列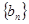 的前
的前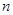 项和
项和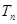 ;
;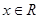 ,恒有
,恒有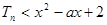 成立,求实数
成立,求实数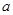 的取值范围
的取值范围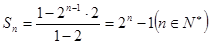 . (2)
. (2)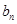
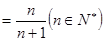
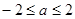
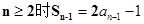 ,再与
,再与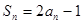 作差可得
作差可得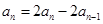 ,进而确定
,进而确定 是等比数列.问题得解.
是等比数列.问题得解.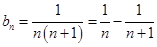 采用裂项求和方法求和.
采用裂项求和方法求和.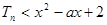 恒成立 , 即
恒成立 , 即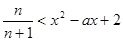 恒成立
恒成立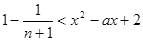 恒成立 ,必须且只须满足
恒成立 ,必须且只须满足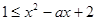 恒成立,然后转化为关于
恒成立,然后转化为关于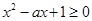 对于一切实数x恒成立即可.
对于一切实数x恒成立即可.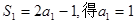 ,…………1分
,…………1分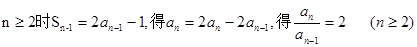 ---------2分
---------2分 是等比数列
是等比数列 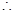 数列
数列 的公比q="2"
的公比q="2"  的通项公式为
的通项公式为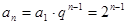
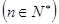 …………3分
…………3分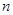 项和公式为
项和公式为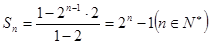 . ………………………4分
. ………………………4分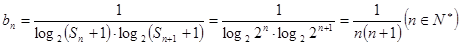
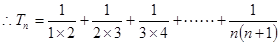 ……………………………6分
……………………………6分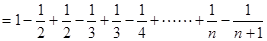 ………………………7分
………………………7分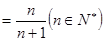 …………………………………………8分
…………………………………………8分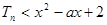 恒成立 即
恒成立 即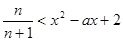 恒成立
恒成立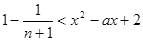 恒成立 ……………………………………9分
恒成立 ……………………………………9分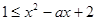 恒成立 ………………………………10分
恒成立 ………………………………10分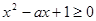 在R上恒成立
在R上恒成立 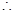
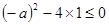 ,………………11分
,………………11分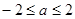 .
. 

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:单选题
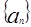 满足
满足 ,则称数列
,则称数列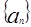 为“等方比数列”甲:数列
为“等方比数列”甲:数列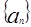 为“等比数列”;乙:数列
为“等比数列”;乙:数列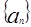 为“等方比数列”;则
为“等方比数列”;则| A.甲是乙的充分不必要条件, |
| B.甲是乙的必要不充分条件, |
| C.甲是乙的充要条件, |
| D.甲既不是乙的充分条件也不是乙的必要条件, |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
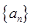 中,
中,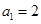 ,
,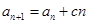 (
(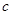 是常数,
是常数,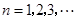 ),且
),且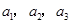 成公比不为
成公比不为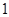 的等比数列。
的等比数列。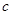 的值;
的值;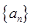 的通项公式。
的通项公式。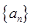 中的第1、3、9、27、……项构成一个新的数列{b
中的第1、3、9、27、……项构成一个新的数列{b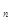 },求
},求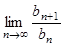 的值。
的值。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
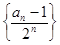 为等差数列;
为等差数列;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com