
下列命题正确的个数( )(1)命题“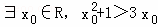 ”的否定是“∀x∈R,x2+1≤3x”;
”的否定是“∀x∈R,x2+1≤3x”;
(2)函数f(x)=cos2ax﹣sin2ax的最小正周期为π”是“a=1”的必要不充分条件;
(3)“x2+2x≥ax在x∈[1,2]上恒成立”⇔“(x2+2x)min≥(ax)max在x∈[1,2]上恒成立”
(4)“平面向量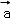 与
与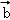 的夹角是钝角”的充分必要条件是“
的夹角是钝角”的充分必要条件是“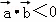 ”A. 1 B. 2 C. 3 D. 4
”A. 1 B. 2 C. 3 D. 4
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
设非常数数列{an}满足an+2=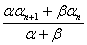 ,n∈N*,其中常数α,β均为非零实数,且α+β≠0.
,n∈N*,其中常数α,β均为非零实数,且α+β≠0.
(1)证明:数列{an}为等差数列的充要条件是α+2β=0;
(2)已知α=1,β=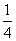 , a1=1,a2=
, a1=1,a2=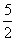 ,求证:数列{| an+1-an-1|} (n∈N*,n≥2)与数列{n+
,求证:数列{| an+1-an-1|} (n∈N*,n≥2)与数列{n+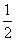 } (n∈N*)中没有相同数值的项.
} (n∈N*)中没有相同数值的项.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知a,b是不共线的向量,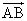 =λa+b,
=λa+b,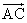 =a+μb(λ,μ∈R),那么A、B、C三点共线的充要条件为( )
=a+μb(λ,μ∈R),那么A、B、C三点共线的充要条件为( )
(A)λ+μ=2 (B)λ-μ=1(C)λμ=-1 (D)λμ=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com