
| A. | (1,2] | B. | (1,$\frac{e+1}{2}$] | C. | (1,$\frac{2e}{3}$] | D. | (1,2) |
分析 把存在唯一的整数x0,使得f(x0)>1,转化为存在唯一的整数x0,使得$\frac{{x}_{0}}{{e}^{{x}_{0}}}-a{x}_{0}+a>1$,即$\frac{{x}_{0}}{{e}^{{x}_{0}}}>a{x}_{0}-a+1$.令g(x)=$\frac{x}{{e}^{x}}$,h(x)=ax-a+1,求得分析g(x)的单调性,作g(x)=$\frac{x}{{e}^{x}}$,h(x)=ax-a+1的图象,数形结合得到$\left\{\begin{array}{l}{h(0)=1-a<0}\\{a≥\frac{1-(-e)}{2}}\end{array}\right.$,则答案可求.
解答 解:f(x)=$\frac{x}{{e}^{x}}$-ax+a,若存在唯一的整数x0,使得f(x0)>1,
即存在唯一的整数x0,使得$\frac{{x}_{0}}{{e}^{{x}_{0}}}-a{x}_{0}+a>1$,也就是存在唯一的整数x0,使得$\frac{{x}_{0}}{{e}^{{x}_{0}}}>a{x}_{0}-a+1$.
令g(x)=$\frac{x}{{e}^{x}}$,h(x)=ax-a+1,
∵g′(x)=$\frac{{e}^{x}-x{e}^{x}}{{e}^{2x}}=\frac{1-x}{{e}^{x}}$,
∴g(x)=$\frac{x}{{e}^{x}}$在(-∞,1]上是增函数,在(1,+∞)上是减函数,
又∵h(x)=ax-a+1是恒过点(1,1)的直线,
∴作g(x)=$\frac{x}{{e}^{x}}$,h(x)=ax-a+1的图象如下,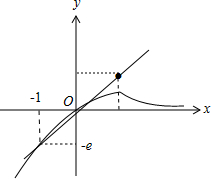
则$\left\{\begin{array}{l}{h(0)=1-a<0}\\{a≥\frac{1-(-e)}{2}}\end{array}\right.$,即1$<a≤\frac{e+1}{2}$.
故选:B.
点评 本题考查利用导数研究函数的单调性,考查根的存在性及根的个数判断,体现了数形结合的解题思想方法,是压轴题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{4}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
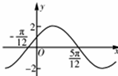 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图,将函数f(x)的图象向左平移$\frac{π}{6}$个单位,得到函数g(x)的图象,则关于函数g(x):
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图,将函数f(x)的图象向左平移$\frac{π}{6}$个单位,得到函数g(x)的图象,则关于函数g(x):| A. | ①③ | B. | ②③ | C. | ①②③ | D. | ①③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com