
分析 将y=f(x+2)的图象右移2个单位,可得y=f(x)的图象,可知图象关于y轴对称.作出函数y=f(x)的图象,由方程的解为f(x)=$\frac{5}{4}$或f(x)=a.作出直线y=$\frac{5}{4}$或y=a.通过图象观察,即可得到所求a的范围.
解答 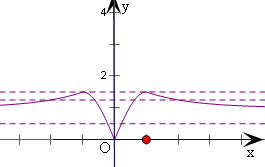 解:y=f(x+2)的函数图象关于x=-2对称,
解:y=f(x+2)的函数图象关于x=-2对称,
将y=f(x+2)的图象右移2个单位,可得y=f(x)的图象,
可知图象关于y轴对称.
作出函数y=f(x)的图象,
关于x的方程4f2(x)-(4a+5)f(x)+5a=0,
即有f(x)=$\frac{5}{4}$或f(x)=a.
y=f(x)和直线y=$\frac{5}{4}$的交点有4个,即f(x)=$\frac{5}{4}$的解的个数为4,由题意可得f(x)=a有两个解.
即y=f(x)和直线y=a有两个交点,
由图象可得a=$\frac{3}{2}$或0<a≤1.
综上可得a的范围是(0,1]∪{$\frac{3}{2}$}.
点评 本题考查函数方程的转化思想的运用,考查方程的根的分布情况,注意运用数形结合的思想方法,属于中档题.


科目:高中数学 来源: 题型:解答题
| 评分等级 | ☆ | ☆☆ | ☆☆☆ | ☆☆☆☆ | ☆☆☆☆☆ |
| 小学 | 2 | 7 | 9 | 20 | 12 |
| 中学 | 3 | 9 | 18 | 12 | 8 |
| 学校类型 | 满意 | 不满意 | 总计 |
| 小学 | 50 | ||
| 中学 | 50 | ||
| 总计 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
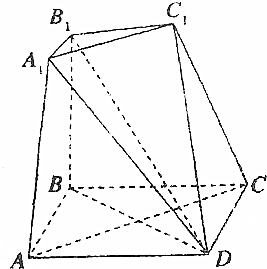 如图所示的七面体是由三棱台ABC-A1B1C1和四棱锥D-AA1C1C对接而成,四边形ABCD是边长为2的正方形,BB1⊥平面⊥ABCD,BB1=2A1B1=2.
如图所示的七面体是由三棱台ABC-A1B1C1和四棱锥D-AA1C1C对接而成,四边形ABCD是边长为2的正方形,BB1⊥平面⊥ABCD,BB1=2A1B1=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 双曲线的一支,这支过点(1,$\frac{1}{2}$) | B. | 抛物线的一部分,这部分过点(1,$\frac{1}{2}$) | ||
| C. | 双曲线的一支,这支过点(-1,$\frac{1}{2}$) | D. | 抛物线的一部分,这部分过点(-1,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若函数f(x)是定义在R上的偶函数,则b=±1 | |
| B. | 若函数f(x)是定义在R上的奇函数,则b=1 | |
| C. | 若b=-1,则函数f(x)是定义在R上的增函数 | |
| D. | 若b=-1,则函数f(x)是定义在R上的减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2] | B. | (1,$\frac{e+1}{2}$] | C. | (1,$\frac{2e}{3}$] | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 年龄x | 6 | 7 | 8 | 9 |
| 身高y | 118 | 126 | 136 | 144 |
| A. | 65 | B. | 74 | C. | 56 | D. | 47 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0<0,e${\;}^{{x}_{0}}$+2x0-1<0 | B. | ?x≥0,ex+2x-1<0 | ||
| C. | ?x0≥0,e${\;}^{{x}_{0}}$+2x0-1<0 | D. | ?x0<0,e${\;}^{{x}_{0}}$+2x0-1≥0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com