
| A. | 若函数f(x)是定义在R上的偶函数,则b=±1 | |
| B. | 若函数f(x)是定义在R上的奇函数,则b=1 | |
| C. | 若b=-1,则函数f(x)是定义在R上的增函数 | |
| D. | 若b=-1,则函数f(x)是定义在R上的减函数 |
分析 由偶函数的定义,可得f(-x)=f(x),化简整理,可得b=0,即可判断A;
由奇函数的定义,可得f(-x)=-f(x),化简整理,可得b=±1,即可判断B;
若b=-1,由换元法和对数函数的单调性,复合函数的单调性,即可判断C,D.
解答 解:对于A,若函数f(x)是定义在R上的偶函数,
可得f(-x)=f(x),即为log${\;}_{\frac{1}{2}}}$($\sqrt{{x^2}+1}$-bx)=log${\;}_{\frac{1}{2}}}$($\sqrt{{x^2}+1}$+bx),
即有$\sqrt{{x^2}+1}$-bx=$\sqrt{{x^2}+1}$+bx,解得b=0,故A错误;
对于B,若函数f(x)是定义在R上的奇函数,
可得f(-x)=-f(x),即为log${\;}_{\frac{1}{2}}}$($\sqrt{{x^2}+1}$-bx)=-log${\;}_{\frac{1}{2}}}$($\sqrt{{x^2}+1}$+bx),
即有$\sqrt{{x^2}+1}$-bx=($\sqrt{{x^2}+1}$+bx)-1,即有x2+1-b2x2=1,
解得b=±1,故B错误;
对于C,若b=-1,则f(x)=log${\;}_{\frac{1}{2}}}$($\sqrt{{x^2}+1}$-x)=log${\;}_{\frac{1}{2}}}$($\sqrt{{x^2}+1}$+x)-1
=log2($\sqrt{{x^2}+1}$+x),由t=$\sqrt{{x^2}+1}$+x在x≥0递增,函数f(x)为奇函数,
可得f(x)在R上递增,故C正确,D错误.
故选:C.
点评 本题考查对数函数的单调性,函数的奇偶性的运用,注意运用定义法,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
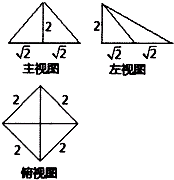
| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{{4\sqrt{2}}}{3}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | r=1,m为偶数 | B. | r=1,m为奇数 | C. | r=-1,m为偶数 | D. | r=-1,m为奇数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{3}{7}$ | B. | $\frac{4}{9}$ | C. | $\frac{9}{20}$ | D. | $\frac{5}{11}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com