
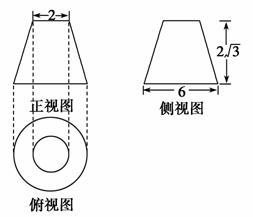
已知某几何体的正视图和侧视图是全等的等腰梯形,俯视图是两个同心圆,如图所示,则该几何体的全面积为________.
 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
双曲线 -
-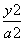 =-1(b>0,a>0)与抛物线y=
=-1(b>0,a>0)与抛物线y=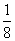 x2有一个公共焦点F,双曲线的过点F且垂直于y轴的弦长为
x2有一个公共焦点F,双曲线的过点F且垂直于y轴的弦长为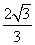 ,则双曲线的离心率等于( )
,则双曲线的离心率等于( )
A.2 B.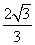
C.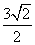 D.
D.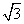
查看答案和解析>>
科目:高中数学 来源: 题型:
若抛物线y2=4x的焦点为F,过F且斜率为1的直线交抛物线于A、B两点,动点P在曲线y2=-4x(y≥0)上,则△PAB的面积的最小值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
若F1,F2是椭圆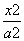 +
+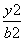 =1(a>2b>0)的两个焦点,分别过F1,F2作倾斜角为45°的两条直线与椭圆相交于四点,以该四点为顶点的四边形和以椭圆的四个顶点为顶点的四边形的面积比等于
=1(a>2b>0)的两个焦点,分别过F1,F2作倾斜角为45°的两条直线与椭圆相交于四点,以该四点为顶点的四边形和以椭圆的四个顶点为顶点的四边形的面积比等于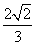 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )
A.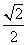 B.
B.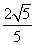
C.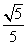 D.
D.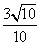
查看答案和解析>>
科目:高中数学 来源: 题型:
在如图所示的几何体中,四边形ABCD是正方形,MA⊥平面ABCD,PD∥MA,E、G、F分别为MB、PB、PC的中点,且AD=PD=2MA.
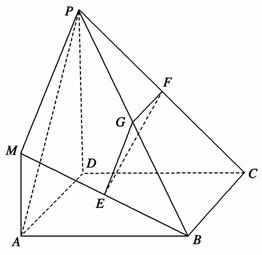
(1)求证:平面EFG⊥平面PDC;
(2)求三棱锥P-MAB与四棱锥P-ABCD的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知四棱锥P-ABCD的正视图是一个底边长为4、腰长为3的等腰三角形,如图分别是四棱锥P-ABCD的侧视图和俯视图.
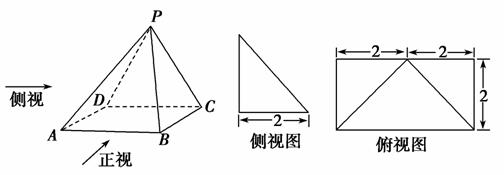
(1)求证:AD⊥PC;
(2)求四棱锥P-ABCD的侧面PAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
.如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
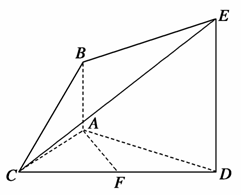
(1)求证:AF∥平面BCE;
(2)求证:平面BCE⊥平面CDE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com