Question

4．已知A，B是单位圆O上的两点（O为圆心），∠AOB=120°，点C是线段AB上不与A、B重合的动点．MN是圆O的一条直径，则$\overrightarrow{CM}$•$\overrightarrow{CN}$的取值范围是（　　）

• A． $[-\frac{3}{4}，0）$
• B． [-1，1）
• C． $[-\frac{1}{2}，1）$
• D． [-1，0）

Answer 1

分析 先根据条件画出图形，根据条件可求出$\frac{1}{2}≤|\overrightarrow{OC}|＜1$，并求出$\overrightarrow{OM}•\overrightarrow{ON}=-1$，$\overrightarrow{OM}+\overrightarrow{ON}=\overrightarrow{0}$，而$\overrightarrow{CM}=\overrightarrow{OM}-\overrightarrow{OC}$，$\overrightarrow{CN}=\overrightarrow{ON}-\overrightarrow{OC}$，带入$\overrightarrow{CM}•\overrightarrow{CN}$并进行数量积的运算便可得到$\overrightarrow{CM}•\overrightarrow{CN}=-1+{\overrightarrow{OC}}^{2}$，这样便可得出$\overrightarrow{CM}•\overrightarrow{CN}$的取值范围．

解答 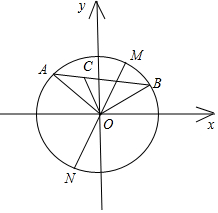解：如图，
∵OA=OB=1，∠AOB=120°；
∴O到直线AB的距离d=$\frac{1}{2}$；
∴$\frac{1}{2}≤|\overrightarrow{OC}|＜1$；
∴$\overrightarrow{CM}•\overrightarrow{CN}=（\overrightarrow{OM}-\overrightarrow{OC}）•（\overrightarrow{ON}-\overrightarrow{OC}）$
=$\overrightarrow{OM}•\overrightarrow{ON}-（\overrightarrow{OM}+\overrightarrow{ON}）•\overrightarrow{OC}+{\overrightarrow{OC}}^{2}$
=$-1+{\overrightarrow{OC}}^{2}$；
∴$-\frac{3}{4}≤\overrightarrow{CM}•\overrightarrow{CN}＜0$；
∴$\overrightarrow{CM}•\overrightarrow{CN}$的取值范围为$[-\frac{3}{4}，0）$．
故选A．

点评 考查单位圆的定义，数形结合解题的方法，向量减法的几何意义，向量数量积的运算，不等式的性质．