
����Ŀ���ֶ�ij�й�н�ײ���ڡ�¥�������̬�Ƚ��е��飬��������50�ˣ������������Ƶ���ֲ����ԡ�¥��������������±���
�����루��λ��Ԫ�� | [15,25 | [25��35 | [35��45 | [45��55 | [55��65 | [65,75 |
Ƶ�� | 5 | 10 | 15 | 10 | 5 | 5 |
������ | 4 | 8 | 12 | 5 | 2 | 1 |
��1��������ͳ������������2![]() 2�������е�
2�������е�![]() ��ֵ�������Ƿ���99%�İ�����Ϊ����������5500Ϊ�ֽ��ԡ�¥����� ��̬���в��죻
��ֵ�������Ƿ���99%�İ�����Ϊ����������5500Ϊ�ֽ��ԡ�¥����� ��̬���в��죻
���������55��Ԫ������ | �����벻����55��Ԫ������ | �ϼ� | |
�� | a | b | |
���� | c | d | |
�ϼ� | 50 |
��2)������[55��65���ڵı������������ѡȡ���˽����ٵ��飬��ѡ�е�2���в��ɡ�¥�����������Ϊ![]() ����
����![]() �ĸ���.
�ĸ���.
����![]() ��
��![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
���𰸡���1������������2��![]()
��������
��1���������![]() �������ɵ�
�������ɵ�![]() ���ɴ˿ɵ������������2�����������ݹŵ�����������
���ɴ˿ɵ������������2�����������ݹŵ�����������
��1���������![]() ��
��
��![]() ��
��
��û��99%�İ�����Ϊ��������5500Ϊ�ֽ��ԡ�¥�������̬���в���.
(2) ��[55��65���ڵ�5�����������У������ɡ�¥������߷ֱ��ΪA,B,����
���ɡ�¥������߷ֱ��ΪC,D,E��
������ѡ��������(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E),(C,D),(C,E),(D,E)����10�ֲ�ͬ���Σ�![]() ��ʾѡ�е�2���в��ɡ�¥�����������Ϊ1������(A,C),(A,D),(A,E),(B,C),(B,D),(B,E)����6�ֲ�ͬ���Σ�
��ʾѡ�е�2���в��ɡ�¥�����������Ϊ1������(A,C),(A,D),(A,E),(B,C),(B,D),(B,E)����6�ֲ�ͬ���Σ�
��![]() �ĸ���Ϊ
�ĸ���Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=|x��1|��|x+2|�� ������ʽ��2��f��x����0�Ľ⼯A��
������m��n��A��֤����|1��4mn|��2|m��n|��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=|x��1|+|x+a|��x��2�� ����a=1ʱ����ʽf��x����0�Ľ⼯��
������a����1���Ҵ���x0��[��a��1����ʹ��f��x0����0����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ijУ���εĺ���֪ʶ�����У����뾺�����Ŀ���������������֮��Ϊ1��3���ҳɼ��ֲ���![]() ��Χ�ڣ��涨������80���ϣ���80����ͬѧ�����������÷ֲ�����ķŷ���ȡ200�˵ijɼ���Ϊ�������õ��ɼ���Ƶ�ʷֲ�ֱ��ͼ.
��Χ�ڣ��涨������80���ϣ���80����ͬѧ�����������÷ֲ�����ķŷ���ȡ200�˵ijɼ���Ϊ�������õ��ɼ���Ƶ�ʷֲ�ֱ��ͼ.
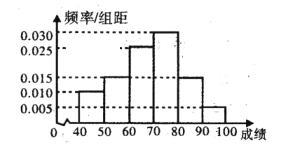
(��)��д����![]() �����������ܷ��г���95%�İ�����Ϊ������ѧ�����������йء���
�����������ܷ��г���95%�İ�����Ϊ������ѧ�����������йء���
(��)�������������õ�Ƶ����Ϊ���ʣ��ִӲ���ѧ���У������ȡ3��ѧ�����ǡ���ѧ������Ϊ![]() ,��
,��![]() �ķֲ��м���ѧ����.
�ķֲ��м���ѧ����.

��������ʽ��![]() ������
������![]()

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���꾭Ӫ��һ����Ʒ���н�����ÿ��10Ԫ������һ�ܵ��������ݵó���������![]() �������뵥��
�������뵥��![]() ��Ԫ��֮��Ĺ�ϵ����ͼ��ʾ����������������Ʒ�йص��ܿ�֧��Ϊ25Ԫ.
��Ԫ��֮��Ĺ�ϵ����ͼ��ʾ����������������Ʒ�йص��ܿ�֧��Ϊ25Ԫ.

��1��������������ͼд��![]() �������뵥��
�������뵥��![]() ��Ԫ��֮��ĺ�����ϵʽ��
��Ԫ��֮��ĺ�����ϵʽ��
��2��д������![]() ��Ԫ���뵥��
��Ԫ���뵥��![]() ��Ԫ��֮��ĺ�����ϵʽ��������Ʒ�����ۼ۸�Ϊ����Ԫʱ�����������������������.
��Ԫ��֮��ĺ�����ϵʽ��������Ʒ�����ۼ۸�Ϊ����Ԫʱ�����������������������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ����
����![]() ��
��![]() ���ҵ�
���ҵ�![]() ������Ϊ
������Ϊ![]() .
.
��1�������![]() ��ֱ�ߵķ��̣�
��ֱ�ߵķ��̣�
��2��������ѧ���ɷ�֤��������![]() ����
����![]() ���ڣ�1���е�ֱ��
���ڣ�1���е�ֱ��![]() ��.
��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��= ![]()
![]() ����������
���������� ![]() =��2cosx��1����
=��2cosx��1���� ![]() =��cosx��
=��cosx�� ![]() sin2x����x��R��
sin2x����x��R��
��1����f��x������С�������뵥���ݼ����䣻
��2���ڡ�ABC�У�a��b��c�ֱ��ǽ�A��B��C�ĶԱߣ���֪f��A��=2��b=1����ABC�����Ϊ ![]() ����
���� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}��ǰn���ΪSn����a1��1��an��1��![]() Sn(n��1��2��3����)��
Sn(n��1��2��3����)��
(1)������{an}��ͨ�ʽ��
(2)��bn��![]() (3an��1)ʱ����֤������
(3an��1)ʱ����֤������![]() ��ǰn���Tn��
��ǰn���Tn��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���У� ��
��1��y=x+ ![]() ��x��R����СֵΪ2��
��x��R����СֵΪ2��
��2��a2+b2��2ab��a��b��R�������
��3��a��b��0��c��d��0�������ac��bd��
��4�����⡰x��R��ʹ��x2+x+1��0���ķ��ǡ�x��R��ʹ��x2+x+1��0����
��5��ʵ��x��y�� ![]() ��
�� ![]() �����ij�Ҫ������
�����ij�Ҫ������
��6����p��qΪ�����⣬����p��q��Ϊ�����⣬�Vp�ũVq��ҲΪ�����⣮
A.2��
B.3��
C.4��
D.5��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com