
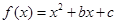 为偶函数,曲线
为偶函数,曲线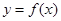 过点
过点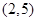 ,
, 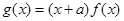 .
.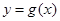 有斜率为0的切线,求实数
有斜率为0的切线,求实数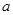 的取值范围;
的取值范围;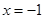 时函数
时函数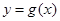 取得极值,确定
取得极值,确定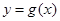 的单调区间.
的单调区间.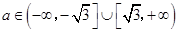 ;(2)
;(2)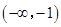 和
和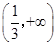 为
为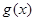 的单调递增区间,
的单调递增区间,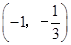 为
为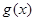 的单调递增区间.
的单调递增区间.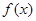 为偶函数,得到
为偶函数,得到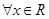 ,恒有
,恒有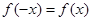 ,进而计算出
,进而计算出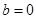 (也可根据二次函数的图像与性质得到对称轴
(也可根据二次函数的图像与性质得到对称轴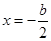 ,该对称轴为
,该对称轴为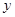 轴,进而得出
轴,进而得出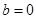 ),然后将点
),然后将点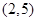 代入求出
代入求出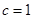 ,进而写出
,进而写出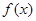 的表达式,此时
的表达式,此时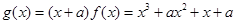 ,根据条件
,根据条件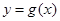 有斜率为0的切线即
有斜率为0的切线即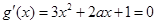 有实数解,根据二次方程有解的条件可得
有实数解,根据二次方程有解的条件可得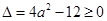 ,求解出
,求解出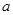 的取值范围即可;(2)先根据
的取值范围即可;(2)先根据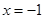 时函数
时函数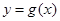 取得极值,得到
取得极值,得到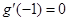 ,进而求出
,进而求出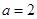 ,然后确定导函数
,然后确定导函数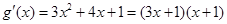 ,由导数
,由导数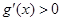 可求出函数的单调增区间,由
可求出函数的单调增区间,由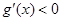 可求出函数的单调减区间.
可求出函数的单调减区间.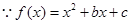 为偶函数,故对
为偶函数,故对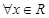 ,总有
,总有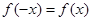 ,易得
,易得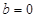
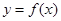 过点
过点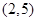 ,得
,得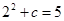 ,得
,得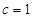 ,
,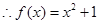 3分
3分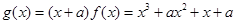
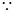 曲线
曲线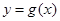 有斜率为0的切线,故
有斜率为0的切线,故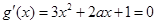 有实数解
有实数解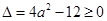 ,解得
,解得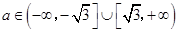 5分
5分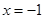 时函数
时函数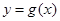 取得极值,故有
取得极值,故有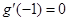 ,解得
,解得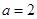
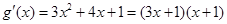 ,令
,令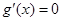 ,得
,得 .
.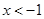 时,
时,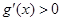
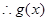 在
在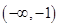 上为增函数
上为增函数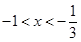 时,
时,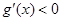 ,
,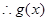 在
在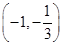 上为减函数
上为减函数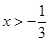 时,
时,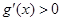 ,
,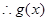 在
在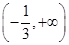 上为增函数
上为增函数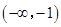 和
和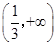 为
为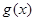 的单调递增区间,
的单调递增区间,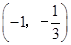 为
为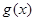 的单调递增区间 10分.
的单调递增区间 10分.

科目:高中数学 来源:不详 题型:填空题
| 1 |
| ax-1 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.f(2)<f(3)<g(0) | B.g(0)<f(3)<f(2) |
| C.f(2)<g(0)<f(3) | D.g(0)<f(2)<f(3) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
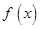 的定义域为D,如果
的定义域为D,如果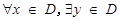 ,使得
,使得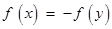
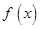 为“Ω函数”. 给出下列四个函数:①
为“Ω函数”. 给出下列四个函数:①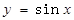 ;
;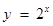 ;③
;③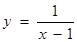 ;④
;④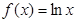 , 则其中“Ω函数”共有( )
, 则其中“Ω函数”共有( )| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
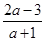 ,则实数a的取值范围是________.
,则实数a的取值范围是________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com