
分析 解法一:(1)求出函数的定义域,求出函数的导数,通过讨论a的范围从而求出函数的单调性;
(2)通过讨论a的范围,确定函数的单调区间,从而求出a的最大值即可.
解法二:(1)出函数的定义域,求出函数的导数,通过讨论a的范围从而求出函数的单调性;
(2)先求出函数f(x)的导数,构造函数g(x)=2ax2-3ax+1,求出g(x)的对称轴以及方程g(x)=0的根,结合函数的单调性求出a的范围即可.
解答 解:解法一:
(1)f(x)=lnx+a(x2-3x+2)的定义域为(0,+∞)…(1分),
$f'(x)=\frac{1}{x}+a(2x-3)$=$\frac{{2a{x^2}-3ax+1}}{x}$,
令g(x)=2ax2-3ax+1…(2分)
①当a=0时,g(x)=1,f′(x)>0在(0,+∞)恒成立,
所以函数f(x)在(0,+∞)上单调递增; …(3分)
②当a>0时,△=9a2-8a=a(9a-8)
当$0<a≤\frac{8}{9}$时,△≤0,g(x)≥0,所以f(x)在(0,+∞)上单调递增; …(4分)
当$a>\frac{8}{9}$时,△>0,g(x)=2ax2-3ax+1=0的两根
为$x_1^{\;}=\frac{{3a-\sqrt{9{a^2}-8a}}}{4a}>0$,$x_2^{\;}=\frac{{3a+\sqrt{9{a^2}-8a}}}{4a}>0$,即0<x1<x2
所以,当x∈(0,x1)时,g(x)>0,f'(x)>0,函数f(x)单调递增;
当x∈(x1,x2)时,g(x)<0,f'(x)<0,函数f(x)单调递减;
当x∈(x2,+∞)时,g(x)>0,f'(x)>0,函数f(x)单调递增; …(5分)
③当a<0时,△=9a2-8a=a(9a-8)>0,g(x)=2ax2-3ax+1=0的两根
为$x_1^{\;}=\frac{{3a-\sqrt{9{a^2}-8a}}}{4a}>0$,$x_2^{\;}=\frac{{3a+\sqrt{9{a^2}-8a}}}{4a}<0$,即x2<0<x1
当x∈(0,x1)时,g(x)>0,f'(x)>0,函数f(x)单调递增;
当x∈(x1,+∞)时,g(x)<0,f'(x)<0,函数f(x)单调递减; …(6分)
综上:当a<0时,函数f(x)在(0,x1)单调递增,函数f(x)在(x1,+∞)单调递减;
当$0≤a≤\frac{8}{9}$时,函数f(x)在(0,+∞)上单调递增;
当$a>\frac{8}{9}$时,函数f(x)在(0,x1)和(x2,+∞)单调递增;函数f(x)在(x1,x2)单调递减 …(7分)
(2)由(1)知
①当$0<a≤\frac{8}{9}$时,函数f(x)在(1,+∞)上单调递增,
因为f(1)=0,所以x∈(1,+∞)时,f(x)>f(1)=0,符合题意; …(8分)
②当$\frac{8}{9}<a≤1$时,$0<\frac{{3a-\sqrt{9{a^2}-8a}}}{4a}$$<\frac{{3a+\sqrt{9{a^2}-8a}}}{4a}≤1$,即0<x1<x2≤1
所以,函数f(x)在(1,+∞)上单调递增,
又f(1)=0,所以x∈(1,+∞)时,f(x)>f(1)=0,符合题意; …(10分)
③当a>1时,$0<\frac{{3a-\sqrt{9{a^2}-8a}}}{4a}<1$$<\frac{{3a+\sqrt{9{a^2}-8a}}}{4a}$,即0<x1<1<x2
由f(1)=0,函数f(x)在(x1,x2)单调递减,
所以x∈(1,x2)时,f(x)<f(1)=0不符合题意,…(11分)
综上所述,a的取值范围是(0,1],所以a的最大值为1.…(12分)
解法二:
(1)f(x)=lnx+a(x2-3x+2)的定义域为(0,+∞)…(1分),
$f'(x)=\frac{1}{x}+a(2x-3)$=$\frac{{2a{x^2}-3ax+1}}{x}$,令g(x)=2ax2-3ax+1…(2分)
①当a=0时,g(x)=1,f′(x)>0在(0,+∞)恒成立,
所以函数f(x)在(0,+∞)上单调递增; …(3分)
②当a>0时,g(x)=2ax2-3ax+1的对称轴为$x=\frac{3}{4}$
若$g(\frac{3}{4})≥0$时,即$0<a≤\frac{8}{9}$,g(x)≥0,f′(x)≥0所以f(x)在(0,+∞)上单调递增; …(4分)
若$g(\frac{3}{4})<0$时,即$a>\frac{8}{9}$,g(x)=2ax2-3ax+1=0的两根
为$x_1^{\;}=\frac{{3a-\sqrt{9{a^2}-8a}}}{4a}>0$,$x_2^{\;}=\frac{{3a+\sqrt{9{a^2}-8a}}}{4a}>0$,即0<x1<x2
所以,当x∈(0,x1)时,g(x)>0,f'(x)>0,函数f(x)单调递增;
当x∈(x1,x2)时,g(x)<0,f'(x)<0,函数f(x)单调递减;
当x∈(x2,+∞)时,g(x)>0,f'(x)>0,函数f(x)单调递增; …(5分)
③当a<0时,△=9a2-8a=a(9a-8)>0,g(x)=2ax2-3ax+1=0的两根
为$x_1^{\;}=\frac{{3a-\sqrt{9{a^2}-8a}}}{4a}>0$,$x_2^{\;}=\frac{{3a+\sqrt{9{a^2}-8a}}}{4a}<0$,即x2<0<x1
当x∈(0,x1)时,g(x)>0,f′(x)>0,函数f(x)单调递增;
当x∈(x1,+∞)时,g(x)<0,f′(x)<0,函数f(x)单调递减; …(6分)
综上:当a<0时,函数f(x)在(0,x1)单调递增,函数f(x)在(x1,+∞)单调递减;
当$0≤a≤\frac{8}{9}$时,函数f(x)在(0,+∞)上单调递增;
当$a>\frac{8}{9}$时,函数f(x)在(0,x1)和(x2,+∞)单调递增;函数f(x)在(x1,x2)单调递减 …(7分)
(2)$f'(x)=\frac{1}{x}+a(2x-3)$=$\frac{{2a{x^2}-3ax+1}}{x}$,因为a>0
令g(x)=2ax2-3ax+1,g(x)的对称轴$x=\frac{3}{4}$,
①当$g(\frac{3}{4})≥0$时,即$0<a≤\frac{8}{9}$,x∈(0,+∞),g(x)≥0,
所以f′(x)>0,即f(x)在(0,+∞)上单调递增,x>1,f(x)>f(1)=0,即$0<a≤\frac{8}{9}$,对?x>1,f(x)≥0成立; …(8分)
②当$g(\frac{3}{4})<0$时,即$a>\frac{8}{9}$,g(x)=2ax2-3ax+1=0的两根为$x_1^{\;}=\frac{{3a-\sqrt{9{a^2}-8a}}}{4a}>0$,$x_2^{\;}=\frac{{3a+\sqrt{9{a^2}-8a}}}{4a}>0$,且0<x1<x2…(9分)
若$x_2^{\;}=\frac{{3a+\sqrt{9{a^2}-8a}}}{4a}≤1$,即$\frac{8}{9}<a≤1$时x∈(1,+∞)时,f′(x)>0,所以函数f(x)在(1,+∞)上单调递增,
又f(1)=0,所以x∈(1,+∞)时,f(x)>f(1)=0,符合题意; …(10分)
若$x_2^{\;}=\frac{{3a+\sqrt{9{a^2}-8a}}}{4a}>1$,即a>1时,$0<\frac{{3a-\sqrt{9{a^2}-8a}}}{4a}<1$$<\frac{{3a+\sqrt{9{a^2}-8a}}}{4a}$,即0<x1<1<x2
由f(1)=0,函数f(x)在(x1,x2)单调递减,
所以x∈(1,x2)时,f(x)<f(1)=0不符合题意,…(11分)
综上所述,a的取值范围是(0,1],所以a的最大值为1.…(12分)
点评 本题考察了函数的单调性、最值问题,考察导数的应用,分类讨论思想,是一道中档题.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
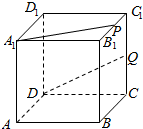 如图,在正方体ABCD-A1B1C1D1中,点P、Q分别是B1C1、CC1的中点,则直线A1P与DQ的位置关系是相交.(填“平行”、“相交”或“异面”)
如图,在正方体ABCD-A1B1C1D1中,点P、Q分别是B1C1、CC1的中点,则直线A1P与DQ的位置关系是相交.(填“平行”、“相交”或“异面”)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
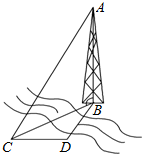 如图,测量河对岸的塔高AB时,选与塔底B在同一水平面内的两个测点C与D,在D点测得塔在北偏东30°方向,然后向正西方向前进10米到达C,测得此时塔在北偏东60°方向.并在点C测得塔顶A的仰角为60°,则塔高AB=30米.
如图,测量河对岸的塔高AB时,选与塔底B在同一水平面内的两个测点C与D,在D点测得塔在北偏东30°方向,然后向正西方向前进10米到达C,测得此时塔在北偏东60°方向.并在点C测得塔顶A的仰角为60°,则塔高AB=30米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
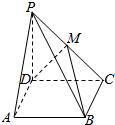 已知四棱锥P-ABCD的底面是平行四边形,如图,M是PC的中点,问向量$\overrightarrow{PA}$、$\overrightarrow{MB}$、$\overrightarrow{MD}$是否可以组成一个基底,并说明理由.
已知四棱锥P-ABCD的底面是平行四边形,如图,M是PC的中点,问向量$\overrightarrow{PA}$、$\overrightarrow{MB}$、$\overrightarrow{MD}$是否可以组成一个基底,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com