S为△ABC所在平面外一点，SA⊥平面ABC，平面SAB⊥平面SBC.求证：AB⊥BC.
科目：高中数学 来源： 题型：
如图所示，SA⊥平面ABC，AB
⊥BC，过A作SB的垂线，垂足为E，过E作SC的垂线，垂足为F.
求证：AF⊥SC.
证明：要证AF⊥SC，只需证SC⊥平
面AEF，只需证AE⊥SC(因为______)，只需证______，只需证AE⊥BC(因为________)，只需证BC⊥平面SAB，只需证BC⊥SA(因为______)．由SA⊥平面ABC可知，上式成立．
查看答案和解析>>
科目：高中数学 来源： 题型：
类比平
面内正三角形的“三边相等，三内角相等”的性质，可推知正四面体的下列性质
中，你认为比较恰当的是________．(填序号)
①各棱长相等，同一顶点上的两条棱的夹角都相等；
②各个面都是全等的正三角形，相邻两个面所成的二面角都相等；
③各个面都是全等的正三角形，同一顶点上的任两条棱的夹角都相等．
查看答案和解析>>
科目：高中数学 来源： 题型：
记Sn为数列{an}的前n项和，给出两个数列：
(Ⅰ)5,3,1，－1，－3，－5，－7，…
(Ⅱ)－14，－10，－6，－2,2,6,10,14,18，…
(1)对于数列(Ⅰ)，计算S1，S2，S4，S5；
对于数列(Ⅱ)，计算S1，S3，S5，S7；
(2)根据上述结果，对于存在正整数k，满足ak＋ak＋1＝0的这一类等差数列{an}的和的规律，猜想一个正确的结论，并加以说明．
查看答案和解析>>
科目：高中数学 来源： 题型：
在平面几何中，△ABC的内角平分线CE分AB所成线段的比为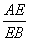
＝
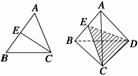
，把这个结论类比到空间：在三棱锥A—BCD中(如图所示)，面DEC平分二面角A—CD—B且与AB相交于E，则得到的类比的结论是________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
证明 如图，作AE⊥SB于E.
的定义域时，第一步推理中大前提是当
有意
，f(1)＝1(x∈N*)，猜想f(x)的表达式为________．
－
>1，求证：
,0)，是否存在常数a、b、c使不等式x≤f(x)≤
对一切实数x均成立？