
记Sn为数列{an}的前n项和,给出两个数列:
(Ⅰ)5,3,1,-1,-3,-5,-7,…
(Ⅱ)-14,-10,-6,-2,2,6,10,14,18,…
(1)对于数列(Ⅰ),计算S1,S2,S4,S5;
对于数列(Ⅱ),计算S1,S3,S5,S7;
(2)根据上述结果,对于存在正整数k,满足ak+ak+1=0的这一类等差数列{an}的和的规律,猜想一个正确的结论,并加以说明.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
先后掷一枚质地均匀骰子(骰子的六个面上分别标有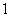 、
、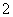 、
、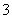 、
、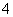 、
、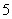 、
、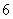 个点)两次,落在水平桌面后,记正面朝上的点数分别为
个点)两次,落在水平桌面后,记正面朝上的点数分别为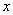 ,
,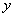 ,设事件
,设事件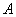 为“
为“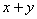 为偶数”, 事件
为偶数”, 事件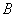 为
为
“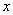 ,
,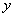 中有偶数且
中有偶数且 ”,则概率
”,则概率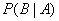 等于 。
等于 。
查看答案和解析>>
科目:高中数学 来源: 题型:
设a,b,c都是正数,则下面关于三个数 a+
a+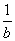 ,b+
,b+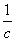 ,c+
,c+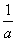 的说法正确的是________.
的说法正确的是________.
①都大于2
②至少有一个大于2
③至少有一个不小于2
④ 至少有一个不大于2
至少有一个不大于2
查看答案和解析>>
科目:高中数学 来源: 题型:
已知在Rt△ABC中,AB⊥AC,AD⊥BC于D,有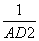 =
=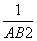 +
+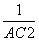 成立.那么在四面体A-BCD中,
成立.那么在四面体A-BCD中, 类比上述结论,你能得到怎样的猜想,说明猜想是否正确及并给出理由.
类比上述结论,你能得到怎样的猜想,说明猜想是否正确及并给出理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知等式:(tan 5°+1)(tan 40°+1)=2;
(tan 15°+1)(tan 30°+1)=2;
(tan 25°+1) (tan 20°+1)=2;
(tan 20°+1)=2;
据此可猜想出一个一般性命题:___ _________________________________________.
_________________________________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
给出演绎推理的“三段论”:
直线平行于平面,则平行于平面内所有的直线;(大前提)
已知直线b∥平面α,直线a⊂平面α;(小前提)
则直线b∥直线a.(结论)
那么这个推理错误的原因是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知命题p:所有有理数都是实数,命题q:正数的对数都是负数,则下列命题中为真命题的序号是________.
(1)(綈p)∨q;(2)p∧q;(3)(綈p)∧(綈q);(4)(綈p)∨(綈q).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com