练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．求证：在同一个圆中，不是直径的两条弦不能相互平分．

    分析 利用反证法假设圆的两条不是直径的相交弦能互相平分，推出矛盾即可．

    解答 证法一：假设圆的两条不是直径的相交弦能互相平分，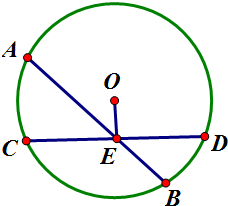
    如图AB，CD为圆O的两条不是直径且互相平分的相交弦，交点为E
    ∵CE=DE，AE=BE，O为圆心
    ∴OE⊥CD，OE⊥AB
    ∴CD∥AB
    显然与AB，CD矛盾，故假设不成立．
    ∴圆的两条不是直径的相交弦不能互相平分．
    证法二：证明：假设AB，CD能互相平分
    连接OE
    ∵AE=BE
    ∴OE⊥AB
    同理OE⊥CD
    因为这与过一点有且有一条直线与已知直线垂直相矛盾，所以假设错误，所以圆的两条不是直径的相交弦不能互相平分．

    点评 此题主要考查了反证法，正确掌握反证法的一般步骤是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    3．已知函数f（x）=$\left\{\begin{array}{l}{1+\frac{1}{x}（x＞1）}\\{{x}^{2}+1（-1≤x≤1）}\\{2x+3（x＜-1）}\end{array}\right.$，若f（a）=$\frac{3}{2}$，则a=a=2或±$\frac{\sqrt{2}}{2}$．．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．在直角坐标系xOy中，直线l的参数方程为$\left\{\begin{array}{l}x=3+\frac{1}{2}t\\ y=\frac{{\sqrt{3}}}{2}t\end{array}\right.（t$为参数），以原点为极点，x轴的正半轴为极轴建立极坐标系，圆C的极坐标方程为$ρ=2\sqrt{3}sinθ$．
    （1）写出圆C的直角坐标方程；
    （2）P为直线l上一动点，当P到圆心C的距离最小时，求P的直角坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．当点P（m，n）为圆x2+（y-2）2=1上任意一点时，不等式m+n+c≥1恒成立，则c的取值范围是（　　）
    A．c≥$\sqrt{2}$-1B．c≤$\sqrt{2}$-1C．-1-$\sqrt{2}$≤c$≤\sqrt{2}-1$D．$\sqrt{2}$-1≤c≤$\sqrt{2}$+1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．同时抛掷两枚骰子，将得到的点数分别记为a，b．
    （1）求a+b=7的概率；
    （2）求点（a，b）在函数y=2x的图象上的概率；
    （3）将a，b，4的值分别作为三条线段的长，将这两枚骰子抛掷三次，ξ表示这三次抛掷中能围成等腰三角形的次数，求ξ的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．以下四个命题
    ①从匀速传递的产品生产流水线上，质检员每5分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样；
    ②样本方差反映了样本数据与样本平均值的偏离程度；
    ③在回归分析模型中，残差平方和越小，说明模型的拟合效果越好；
    ④在回归直线方程$\widehat{y}$=0.1x+10中，当解释变量x每增加一个单位时，预报变量$\widehat{y}$增加0.1个单位．
    其中正确的是（　　）
    A．②③④B．①③④C．①②③D．①②④

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．若sinα=$-\frac{3}{5}$，α是第四象限的角，则$cos（\frac{π}{4}+α）$=（　　）
    A．$-\frac{{7\sqrt{2}}}{10}$B．$\frac{{7\sqrt{2}}}{10}$C．$-\frac{{\sqrt{2}}}{10}$D．$\frac{{\sqrt{2}}}{10}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0}）$的离心率为$\frac{{\sqrt{3}}}{2}$，其右焦点F到直线x-y+$\sqrt{3}$=0的距离为$\sqrt{6}$．
    （Ⅰ）求椭圆C的标准方程；
    （Ⅱ）过椭圆C的右焦点F作倾斜角为45°的直线交C于M，N两点，求三角形OMN的面积（O为坐标原点）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知两角和的余弦公式C（α+β）：cos（α-β）=cosαcosβ-sinαsinβ；
    1．由C（α+β）推导两角和的正弦公式S（α+β）：sin（α+β）=sinαcosβ+cosαsinβ
    2．已知cosα=-$\frac{4}{5}$，α∈（π，$\frac{3}{2}$π），tan β=-$\frac{1}{3}$，β∈（$\frac{π}{2}$，π），求sin（α+β）．

    查看答案和解析>>

    同步练习册答案