
分析 (1)2Sn=(an+3)(an-2)(n∈N*),即2Sn=${a}_{n}^{2}+{a}_{n}-6$,利用递推式化为:(an+an-1)(an-an-1-1)=0,由于an>0,可得an-an-1=1,利用等差数列的通项公式即可得出;
(2)由(1)可得:$\frac{1}{{a}_{2n-1}•{a}_{2n+1}}$=$\frac{1}{2}(\frac{1}{2n+1}-\frac{1}{2n+3})$.利用“裂项求和”即可得出.
解答 解:(1)∵2Sn=(an+3)(an-2)(n∈N*),即2Sn=${a}_{n}^{2}+{a}_{n}-6$,
∴当n=1时,$2{a}_{1}={a}_{1}^{2}+{a}_{1}$-6,a1>0,解得a1=3.
当n≥2时,2Sn-1=${a}_{n-1}^{2}+{a}_{n-1}$-6,
∴2an=${a}_{n}^{2}+{a}_{n}$-${a}_{n-1}^{2}$-an-1,化为(an+an-1)(an-an-1-1)=0,
∵an>0,∴an-an-1=1,∴数列{an}是等差数列,首项为3,公差为1,
∴an=3+(n-1)=n+2,
∴an=n+2.
(2)由(1)可得:$\frac{1}{{a}_{2n-1}•{a}_{2n+1}}$=$\frac{1}{(2n+1)(2n+3)}$=$\frac{1}{2}(\frac{1}{2n+1}-\frac{1}{2n+3})$.
∴数列{$\frac{1}{{a}_{2n-1}•{a}_{2n+1}}$}的前n项和Tn=$\frac{1}{2}[(\frac{1}{3}-\frac{1}{5})+(\frac{1}{5}-\frac{1}{7})$+…+$(\frac{1}{2n+1}-\frac{1}{2n+3})]$=$\frac{1}{2}$$(\frac{1}{3}-\frac{1}{2n+3})$=$\frac{n}{3(2n+3)}$.
点评 本题考查了等差数列的通项公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
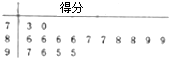 钓鱼岛及其附近海域自古以来就是中国人民进行捕鱼、避风、休息的场所,被誉为深海中的翡翠.某学校就钓鱼岛有关常识随机抽取了16名学生进行测试,用“10分制”以茎叶图方式记录了他们对钓鱼岛的了解程度,分数以小数点前的一位数字为茎,小数点后的一位数字为叶.
钓鱼岛及其附近海域自古以来就是中国人民进行捕鱼、避风、休息的场所,被誉为深海中的翡翠.某学校就钓鱼岛有关常识随机抽取了16名学生进行测试,用“10分制”以茎叶图方式记录了他们对钓鱼岛的了解程度,分数以小数点前的一位数字为茎,小数点后的一位数字为叶.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢足球 | 不喜欢足球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
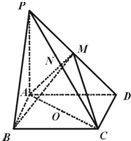 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.若M,N分别为棱PD,PC上的点,O为AC的中点,且AC=2OM=2ON.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.若M,N分别为棱PD,PC上的点,O为AC的中点,且AC=2OM=2ON.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (e,+∞) | B. | [2,e) | C. | $({e+\frac{1}{e},+∞})$ | D. | $[{2,e+\frac{1}{e}})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com