
| A. | y=-$\frac{1}{x}$ | B. | y=ln(x+5) | C. | y=x2-1 | D. | y=x|x| |
分析 根据反比例函数在定义域上的单调性,奇函数图象的对称性便可判断出A,B,C都错误,从而得出D正确.
解答 解:A.$y=-\frac{1}{x}$在定义域内没有单调性,∴该选项错误;
B.y=ln(x+5)的图象不关于原点对称,不是奇函数,∴该选项错误;
C.y=x2-1是偶函数,不是奇函数,∴该选项错误;
D.设y=f(x),f(x)定义域为R,且f(-x)=-x|-x|=-x|x|=-f(x);
∴f(x)为奇函数;
$f(x)=x|x|=\left\{\begin{array}{l}{{x}^{2}}&{x≥0}\\{-{x}^{2}}&{x<0}\end{array}\right.$;
∴f(x)在[0,+∞)上单调递增,在(-∞,0)上单调递增,且02=-02;
∴f(x)在定义域R上是增函数,∴该选项正确.
故选:D.
点评 考查反比例函数在定义域上的单调性,奇函数图象的对称性,熟悉对数函数和二次函数的图象,熟悉平移变换,以及奇函数的定义,含绝对值函数的处理方法:去绝对值号,二次函数的单调性,以及分段函数单调性的判断.


 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2] | B. | $[\frac{1}{2},2]$ | C. | $[\frac{1}{2},2016]$ | D. | R |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
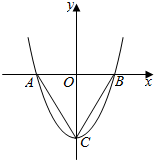 如图.在平面直角坐标系中,O是坐标原点,二次函数y=x2+c的图象抛物线交x轴于点A、B,(点A在点B的左侧),与y轴交点C(0,-3).
如图.在平面直角坐标系中,O是坐标原点,二次函数y=x2+c的图象抛物线交x轴于点A、B,(点A在点B的左侧),与y轴交点C(0,-3).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com