
分析 (1)由题意可知:$x∈[{0,\frac{π}{2}}]$,$sin({2x+\frac{π}{6}})∈[{-\frac{1}{2},1}]$,$-2asin({2x+\frac{π}{6}})∈[{-2a,a}]$,f(x)∈[b,3a+b],由题意即可求得a和b的值,求得函数f(x)的解析式,求得g(x)的解析式,由对数函数的性质可知g(x)>1,由正弦函数图象可知,即可求得g(x)的单调递增区间;
(2)由(1)可知,$f(x)=-4sin({2x+\frac{π}{6}})-1$,$x∈({0,\frac{π}{6}}]$,$sin({2x+\frac{π}{6}})∈(\frac{1}{2},1]$,即可求得f(x)∈[-5,-3),$\left\{\begin{array}{l}{m<3+f(x)}\\{m>f(x)-3}\end{array}\right.$恒成立,即$\left\{\begin{array}{l}{m<3+f(x)_{min}}\\{m>f(x)_{max}-3}\end{array}\right.$,即可求得实数m的取值范围.
解答 (1)∵$x∈[{0,\frac{π}{2}}]$,
∴$2x+\frac{π}{6}∈[{\frac{π}{6},\frac{7π}{6}}]$,
∴$sin({2x+\frac{π}{6}})∈[{-\frac{1}{2},1}]$ …1分
∴$-2asin({2x+\frac{π}{6}})∈[{-2a,a}]$,
∴f(x)∈[b,3a+b]…2分
又∵-5≤f(x)≤1,
∴b=-5,3a+b=1,
∴a=2,b=-5 …4分
$f(x)=-4sin({2x+\frac{π}{6}})-1$,$g(x)=4sin({2x+\frac{π}{6}})-1$ …5分
∵lgg(x)>0,
∴g(x)>1,
∴$sin({2x+\frac{π}{6}})>\frac{1}{2}$,
∴$2kπ+\frac{π}{6}<2x+\frac{π}{6}<2kπ+\frac{5π}{6},k∈Z$ …6分
∵g(x) 单调递增,…7分
∴g(x) 的单调递增区间为$({kπ,kπ+\frac{π}{6}}),k∈Z$ …8分
(2)$f(x)=-4sin({2x+\frac{π}{6}})-1$,$x∈({0,\frac{π}{6}}]$,
∴$2x+\frac{π}{6}∈(\frac{π}{6},\frac{π}{2}]$,
∴$sin({2x+\frac{π}{6}})∈(\frac{1}{2},1]$,
∴f(x)∈[-5,-3)…9分
∵|f(x)-m|<3 对于任意$x∈({0,\frac{π}{6}}]$ 恒成立,等价于$\left\{\begin{array}{l}{m<3+f(x)}\\{m>f(x)-3}\end{array}\right.$恒成立 …10分
即$\left\{\begin{array}{l}{m<3+f(x)_{min}}\\{m>f(x)_{max}-3}\end{array}\right.$…11分
∴-6≤m<-2.
点评 本题考查正弦函图象及性质,正弦函数单调性及最值,考查不等式恒成立,考查转化思想,考查分析问题及解决问题的能力,属于中档题.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:选择题
| A. | $y=-\frac{1}{4}x+\frac{1}{2}$ | B. | $y=-\frac{1}{4}x$ | C. | $y=\frac{1}{4}x+\frac{1}{2}$ | D. | $y=\frac{1}{4}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f:x→y=$\frac{1}{6}$x | B. | f:x→y=$\frac{1}{3}$x | C. | f:x→y=$\frac{1}{2}$x | D. | f:x→y=x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
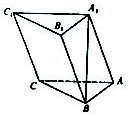 如图,在三棱柱ABC-A1B1C1中,AB⊥AC,顶点A1在底面ABC上的射影恰为点B,且AB=AC=A1B=2.
如图,在三棱柱ABC-A1B1C1中,AB⊥AC,顶点A1在底面ABC上的射影恰为点B,且AB=AC=A1B=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
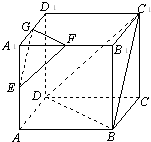 已知正方体ABCD-A1B1C1D1的棱长为2,E、F、G分别是AA1、A1B1、A1D1的中点.
已知正方体ABCD-A1B1C1D1的棱长为2,E、F、G分别是AA1、A1B1、A1D1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com