
����Ŀ��ij����һ�������˾Ϊ�˵���A��B���ֳ��͵ij���������������ȡ�������ֳ���100�����ֱ�ͳ����ÿ����ij�������ڵij���������ͳ���������±���
A���� B����
�������� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | �������� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
������ | 5 | 10 | 30 | 35 | 15 | 3 | 2 | ������ | 14 | 20 | 20 | 16 | 15 | 10 | 5 |
���ӳ�������Ϊ3�������������A��B���ֳ��ͣ��������ȡһ����������������ǡ����A�ͳ��ĸ��ʣ�
������������ڵ�ͳ�����ݣ����Ƹù�˾һ��A�ͳ���һ��B�ͳ�һ���ںϼƳ�������ǡ��Ϊ4��ĸ��ʣ�
����
��������д��A��B���ֳ��͵ij��������ķֲ��м���ѧ������
������������ֳ���ÿ����ÿ������õ�������ͬ���ù�˾��Ҫ��A��B���ֳ����й���һ����ע�����ֳ��͵IJɹ��۸��൱�������������ѧ��ͳ��֪ʶ������Ӧ�ù�����һ�ֳ��ͣ���˵��������ɣ�
���𰸡�����0.6; ����![]() ;����������������������ѡ��A��͵ij�����Ӻ���.
;����������������������ѡ��A��͵ij�����Ӻ���.
�������������������1�����ùŵ���͵ĸ��ʼ��㹫ʽ��⼴�ɣ�2���ù�˾һ��A�ͳ���һ��B�ͳ�һ���ںϼƳ�������ǡ��Ϊ4���Ϊ�������������A�ͳ�1��B�ͳ�3�죬A�ͳ�2��B�ͳ�2�죬A�ͳ�3��B�ͳ�1�죬���û����¼��Ͷ����¼��ĸ��ʼ��㹫ʽ���ã�3������ѧ�����ͷ���������ɵó�����
���������
��������������A�ͳ��ĸ���ԼΪ![]()
������������A�ͳ��ĸ���Ϊ0.6
�����衰�¼�![]() ��ʾһ��A�ͳ���һ���ڳ�������ǡ��Ϊi�족�� ���¼�
��ʾһ��A�ͳ���һ���ڳ�������ǡ��Ϊi�족�� ���¼�![]() ��ʾһ��B�ͳ���һ���ڳ�������ǡ��Ϊj�족������
��ʾһ��B�ͳ���һ���ڳ�������ǡ��Ϊj�족������![]() ����ù�˾һ��A�ͳ���һ��B�ͳ�һ���ںϼƳ�������ǡ��Ϊ4��ĸ���Ϊ
����ù�˾һ��A�ͳ���һ��B�ͳ�һ���ںϼƳ�������ǡ��Ϊ4��ĸ���Ϊ
![]()
![]()
![]()
�ʸù�˾һ��A�ͳ���һ��B�ͳ�һ���ںϼƳ�������ǡ��Ϊ
4��ĸ���Ϊ![]()
����������XΪA�ͳ��������������X�ķֲ���Ϊ
X | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
P | 0.05 | 0.10 | 0.30 | 0.35 | 0.15 | 0.03 | 0.02 |
��YΪB�ͳ��������������Y�ķֲ���Ϊ
Y | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
P | 0.14 | 0.20 | 0.20 | 0.16 | 0.15 | 0.10 | 0.05 |
������һ��A��͵ij��һ�����ڳ���������ƽ��ֵΪ3.62�죬B��͵ij��һ�����ڳ���������ƽ��ֵΪ3.48�죬��ѡ��A��͵ij�����Ӻ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
��������ABEF�У�AB��EF��AB��2��AD��AF��1��AF��BF��OΪAB���е㣬����ABCD ���ڵ�ƽ���ƽ��ABEF���ഹֱ��
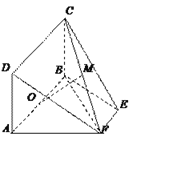
(1)��֤��AF��ƽ��CBF��
(2)��FC���е�ΪM����֤��OM��ƽ��DAF��
(3)������C��BEF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������![]() ������һ������
������һ������![]() ��ʹ�ò���ʽ
��ʹ�ò���ʽ![]() ����������
����������![]() ��
��![]() �����.
�����.
��1���Ը����������![]() ��ֵ��
��ֵ��
��2���ڣ�1�����ý��۵�������֤������![]() ��
��
��3�������������⣬ijͬѧ��ȷ�ز���������![]() ��������һ������
��������һ������![]() ��ʹ�ò���ʽ
��ʹ�ò���ʽ![]() ����������
����������![]() ��
��![]() ��
��![]() ����������۲�����
����������۲�����![]() ������
������![]() �Ĺ��ɣ������������
�Ĺ��ɣ������������![]() ��
��![]() ��
��![]() ��
��![]() ��ص����⣮
��ص����⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾Ϊ��Ƹ��Ա�������һ�����Է�����ӦƸ�ߴ�6����ѡ����һ���������ȡ3���⣬����ĿҪ��������.�涨��������ȷ�������2����ı��ͨ��.��֪6����ѡ����ӦƸ����4��������ȷ��ɣ�2���ⲻ����ɣ�ӦƸ����ÿ����ȷ��ɵĸ��ʶ���![]() ����ÿ����ȷ������Ӱ��.
����ÿ����ȷ������Ӱ��.
��1���ֱ���ס���������ȷ������������ķֲ��м���ѧ������
��2��������Ƚϼס�������˭����ͨ���Ŀ����Դ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����M={��x��y��|y=f��x��}�����������⣨x1��y1����M�����ڣ�x2��y2����M��ʹ��x1x2+y1y2=0��������Ƽ���M�ǡ���ֱ�Ե㼯�������������ĸ����ϣ�
��M={![]() }����M={��x��y��|y=sinx+1}��
}����M={��x��y��|y=sinx+1}��
��M={��x��y��|y=log2x}����M={��x��y��|y=ex��2}��
�����ǡ���ֱ�Ե㼯��������ǣ�������
A. �٢� B. �ڢ� C. �٢� D. �ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() .
.
��1��������������ԭ���ֱ��![]() ��Բ
��Բ![]() ���У���ֱ��
���У���ֱ��![]() �����������ϵĽؾ���ȣ���ֱ��
�����������ϵĽؾ���ȣ���ֱ��![]() �ķ��̣�
�ķ��̣�
��2�����![]() ��Բ
��Բ![]() �ϣ����
�ϣ����![]() ��ֱ��
��ֱ��![]() ��������ֵ����Сֵ.
��������ֵ����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ����( )
A. ��![]() Ϊ�桱�ǡ�
Ϊ�桱�ǡ�![]() Ϊ�桱�ij�ֲ���Ҫ������
Ϊ�桱�ij�ֲ���Ҫ������
B. ����![]() �ı�����3.3��
�ı�����3.3��
C. K2�������ж�������������Ƿ���ص������������K2��ֵ��Сʱ�����ƶ������������أ�
D. ����һ���ع�ֱ�߷���Ϊ![]() �������
�������![]() ÿ����һ����λ��
ÿ����һ����λ��![]() ƽ������1.5����λ.
ƽ������1.5����λ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() ��
��
��1������![]() ʱ������
ʱ������![]() ��ͼ�����ֱ��
��ͼ�����ֱ��![]() �Ϸ�����ʵ��
�Ϸ�����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����֤��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,����·![]() ��Ϊ
��Ϊ![]() ,��
,��![]() ,�������
,�������![]() ����
����![]() ,����
,����![]() �ϵľ��
�ϵľ��![]() Ϊ
Ϊ![]() �ĵ�
�ĵ�![]() ����һ��·��
����һ��·��![]() ,��֪��λ�������·�˷�Ϊ
,��֪��λ�������·�˷�Ϊ![]() ,��·�˷�Ϊ
,��·�˷�Ϊ![]() .
.
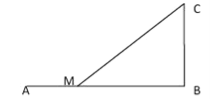
��1�������˷�![]() ��ʾΪ
��ʾΪ![]() �ĺ�����
�����
��2�����ѡ��![]() ��ʹ���˷���С��
��ʹ���˷���С��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com