
【题目】已知集合M={(x,y)|y=f(x)},若对于任意(x1,y1)∈M,存在(x2,y2)∈M,使得x1x2+y1y2=0成立,则称集合M是“垂直对点集”.给出下列四个集合:
①M={![]() };②M={(x,y)|y=sinx+1};
};②M={(x,y)|y=sinx+1};
③M={(x,y)|y=log2x};④M={(x,y)|y=ex﹣2}.
其中是“垂直对点集”的序号是( )
A. ①② B. ②③ C. ①④ D. ②④
【答案】D
【解析】由题意可知,若集合M是“垂直对点集”,则曲线y=f(x)上过任意一点与原点的直线,都存在过另一点与原点的直线与之垂直.
对于①,假设集合![]() 是“垂直对点集”,则存在两点
是“垂直对点集”,则存在两点 ,满足
,满足![]() ,即
,即![]() ,此方程无解。因此,假设不成立,即集合
,此方程无解。因此,假设不成立,即集合![]() 不是“垂直对点集”。
不是“垂直对点集”。
对于②,画出函数![]() 的图象,可得图象向左向右无限伸展,且与x轴相切,在函数
的图象,可得图象向左向右无限伸展,且与x轴相切,在函数![]() 图象上任取一点A,连OA,过原点作直线OA的垂线OB,则直线OB总会与
图象上任取一点A,连OA,过原点作直线OA的垂线OB,则直线OB总会与![]() 的图象相交,所以集合M={(x,y)|y=sinx+1}是“垂直对点集”。
的图象相交,所以集合M={(x,y)|y=sinx+1}是“垂直对点集”。
对于③,在函数![]() 图象上取点(1,0),则在曲线
图象上取点(1,0),则在曲线![]() 不存在点
不存在点![]()
![]() ,满足
,满足![]() ,故集合M={(x,y)|y=log2x}不是“垂直对点集”。
,故集合M={(x,y)|y=log2x}不是“垂直对点集”。
对于④,函数![]() 的图象过点
的图象过点![]() ,且向右上和左下无限伸展,在函数
,且向右上和左下无限伸展,在函数![]() 的图象上任取一点A,连OA,过原点作直线OA的垂线OB,则直线OB总会与
的图象上任取一点A,连OA,过原点作直线OA的垂线OB,则直线OB总会与![]() 的图象相交,所以集合M={(x,y)|y=ex﹣2}是“垂直对点集”。
的图象相交,所以集合M={(x,y)|y=ex﹣2}是“垂直对点集”。


科目:高中数学 来源: 题型:
【题目】如图所示,某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,其中,频率分布直方图的分组区间分别为![]() ,据此解答如下问题.
,据此解答如下问题.
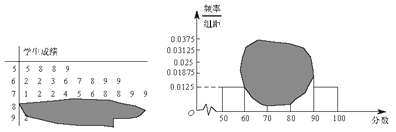
(Ⅰ)求全班人数及分数在![]() 之间的频率;
之间的频率;
(Ⅱ)现从分数在![]() 之间的试卷中任取 3 份分析学生情况,设抽取的试卷分数在
之间的试卷中任取 3 份分析学生情况,设抽取的试卷分数在![]() 的份数为
的份数为![]() ,求
,求![]() 的分布列和数学望期.
的分布列和数学望期.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若曲线![]() 在
在![]() 处的切线的方程为
处的切线的方程为![]() ,求实数
,求实数![]() 的值;
的值;
(2)设![]() ,若对任意两个不等的正数
,若对任意两个不等的正数![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市一汽车出租公司为了调查A,B两种车型的出租情况,现随机抽取了这两种车型各100辆,分别统计了每辆车某个星期内的出租天数,统计数据如下表:
A车型 B车型
出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
车辆数 | 5 | 10 | 30 | 35 | 15 | 3 | 2 | 车辆数 | 14 | 20 | 20 | 16 | 15 | 10 | 5 |
(Ⅰ)从出租天数为3天的汽车(仅限A,B两种车型)中随机抽取一辆,估计这辆汽车恰好是A型车的概率;
(Ⅱ)根据这个星期的统计数据,估计该公司一辆A型车,一辆B型车一周内合计出租天数恰好为4天的概率;
(Ⅲ)
(ⅰ)试写出A,B两种车型的出租天数的分布列及数学期望;
(ⅱ)如果两种车辆每辆车每天出租获得的利润相同,该公司需要从A,B两种车型中购买一辆(注:两种车型的采购价格相当),请你根据所学的统计知识,建议应该购买哪一种车型,并说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图甲,直角梯形![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 分别在
分别在![]() 上,且
上,且![]() ,
, ![]() ,
, ![]() ,现将梯形
,现将梯形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 与平面
与平面![]() 垂直(如图乙).
垂直(如图乙).
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
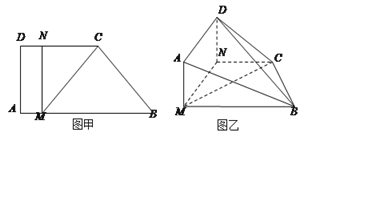
(II)当![]() 的长为何值时,二面角
的长为何值时,二面角![]() 的大小为
的大小为![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费,超过200度但不超过400度的部分按0.8元/度收费,超过400度的部分按1.0元/度收费.
(1)求某户居民用电费用![]() (单位:元)关于月用电量
(单位:元)关于月用电量![]() (单位:度)的函数解析式;
(单位:度)的函数解析式;
(2)为了了解居民的用电情况,通过抽样,获得了今年1月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年1月份用电费用不超过260元的点80%,求![]() 的值;
的值;

(3)在满足(2)的条件下,估计1月份该市居民用户平均用电费用(同一组中的数据用该组区间的中点值作代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,点P(0,1)和点A(m,n)(m≠0)都在椭圆C上,直线PA交x轴于点M.
,点P(0,1)和点A(m,n)(m≠0)都在椭圆C上,直线PA交x轴于点M.
(1)求椭圆C的方程,并求点M的坐标(用m,n表示);
(2)设O为原点,点B与点A关于x轴对称,直线PB交x轴于点N.问:y轴上是否存在点Q,使得∠OQM=∠ONQ?若存在,求点Q的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com