
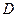 上的函数
上的函数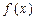 ,如果满足:对任意
,如果满足:对任意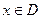 ,存在常数
,存在常数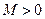 ,都有
,都有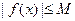 成立,则称
成立,则称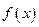 是
是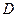 上的有界函数,其中
上的有界函数,其中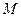 称为函数
称为函数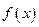 的上界.
的上界.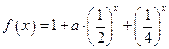 ;
;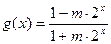 .
. 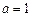 时,求函数
时,求函数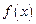 在
在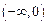 上的值域,并判断函数
上的值域,并判断函数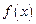 在
在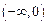 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;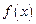 在
在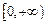 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数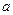 的取值范围;
的取值范围;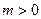 ,函数
,函数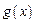 在
在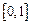 上的上界是
上的上界是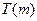 ,求
,求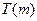 的取值范围.
的取值范围. 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源:不详 题型:解答题
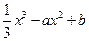 在x=-2处有极值.
在x=-2处有极值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 在
在 上的单调性;
上的单调性; ,使
,使 ,则称
,则称 为函数
为函数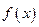 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值; 在
在 上恒成立 , 求
上恒成立 , 求 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
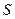 元,用电炉烧开水每吨开水费为
元,用电炉烧开水每吨开水费为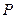 元,
元,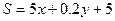 ,
,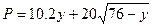 ;其中
;其中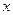 为每吨煤的价格(单位:元),
为每吨煤的价格(单位:元),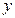 为每百度电的价格(单位:元),如果烧煤时的费用不超过用电炉时的费用,则仍用原备的锅炉烧水,否则就用电炉烧水.
为每百度电的价格(单位:元),如果烧煤时的费用不超过用电炉时的费用,则仍用原备的锅炉烧水,否则就用电炉烧水.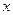 表示为每百度电价
表示为每百度电价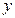 的函数;
的函数;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com